1. UN 2008
Diketahui kubus ABCD.EFGH dengan panjang rusuk 8 cm. Jarak titik H ke garis AC adalah ...
A.  8√3
B.  8√2
C.  4√6
D.  4√3
E.  4√2
Pembahasan :

Jarak titik H ke garis AC adalah OH.
rusuk = a = 8
OH = a2<?XML:NAMESPACE PREFIX = "[default] http://www.w3.org/1998/Math/MathML" NS = "http://www.w3.org/1998/Math/MathML" />a2√6 = 8282√6 = 4√6
Jawaban : C
2. UN 2010
Diketahui kubus ABCD.EFGH dengan panjang rusuk 4 cm. Titik P adalah titik potong AH dan ED dan titik Q adalah titik potong FH dan EG. Jarak titik B ke garis PQ adalah ...
A.  √22  cm
B.  √21  cm
C.  2√5  cm
D.  √19  cm
E.  3√2  cm
Pembahasan :

Jarak titik B ke garis PQ adalah BR.
rusuk = a = 4
BP = BQ = a2a2√6 = 4242√6 = 2√6
PQ = √PS2+SQ2=√22+22=2√2PS2+SQ2=22+22=22
BPQ sama kaki sehingga :
PR = RQ = 1212PQ = 1212(2√2) = √2
Perhatikan segitiga BPR siku-siku di R
BR = √BP2−PR2BP2−PR2
BR = √(2√6)2−(√2)2(26)2−(2)2
BR = √2222
Jawaban : A
3. UN 2011
Diketahui kubus ABCD.EFGH dengan rusuk 8 cm. M adalah titik tengah EH. Jarak titik M ke AG adalah ...
A.  4√6  cm
B.  4√5  cm
C.  4√3  cm
D.  4√2  cm
E.  4  cm
Pembahasan :

Jarak titik M ke garis AG adalah MO
a = 8
Perhatikan bahwa garis MN dan AG berpotongan tegak lurus dan sama besar di titik O, sehingga
MO = 1212. MN
MO = 1212. a√2
MO = 1212. 8√2
MO = 4√2
Jawaban : D
4.  UN 2007
Diketahui kubus ABCD.EFGH dengan rusuk 6√3 cm. Jarak Bidang ACH dan EGB adalah ...
A.  4√3  cm
B.  2√3  cm
C.  4  cm
D.  6  cm
E.  12  cm
Pembahasan :

Jarak bidang ACH dan EGB = jarak garis OH dan BR = jarak titik P dan Q  ⇒ PQ.
rusuk = a = 6√3
OH = BR = a2a2√6 = 9√2
OR = a = 6√3
HF = a√2 = 6√6
HR = 1212 × HF = 3√6
DF = a√3 = 18
Perhatikan bidang BDHF

OHRB adalah jajar genjang dengan alas OH dan tinggi PQ
Ingat : luas jajar genjang =alas×tinggi=alas×tinggi
Luas jajar genjang OHRB = 2 × luas ⊿ OHR
OH × PQ = 2 × 1212×HR×OR
OH × PQ = HR × OR
9√2 × PQ = 3√6 × 6√3
⇒ PQ = 6
atau
DP = PQ = QF = 1313 × DF
DP = PQ = QF = 1313 × 18
⇒ PQ = 6
Jawaban : D
5. UN 2009
Diketahui kubus ABCD.EFGH, panjang rusuk kubus adalah 12 cm. Titik P terletak pada perpanjangan rusuk DC sehingga CP : DP = 1 : 3. Jarak titik P dengan bidang BDHF adalah ...
A.  6√2  cm
B.  9√2  cm
C.  12√2  cm
D.  16√2  cm
E.  18√2  cm
Pembahasan :

Jarak titik P ke bidang BDHF = jarak titik P ke garis BD  ⇒ PQ.
rusuk = a = 12
CP : DP = 1 : 3  ⇒  DC : CP = 2 : 1
DC = 12  ⇒ CP = 6
DP = DC + CP = 12 + 6 =18
BD = a√2 = 12√2
Perhatikan segitiga BDP

Dengan menggunakan rumus luas segitiga diperoleh :
1212 × BD × PQ = 1212 × DP × BC
BD × PQ = DP × BC
12√2 × PQ = 18 × 12
⇒ PQ = 9√2

Jawaban : B

6. UN 2012
Kubus ABCD.EFGH dengan rusuk 4 cm. Jarak titik H ke bidang ACF adalah ...
A.  2323√3  cm
B.  4343√3  cm
C.  113113√3  cm
D.  8383√3  cm
E.  133133√3  cm
Pembahasan :

Jarak titik H ke bidang ACF = jarak titik H ke garis OF = jarak titik H ke titik P  ⇒ HP.
rusuk = a = 4
OF = OH = a2a2√6 = 2√6
FH = a√2 = 4√2
OQ = a = 4
Perhatikan segitiga OFH

HP dan OQ merupakan garis tinggi, sehingga dengan menggunakan rumus luas segitiga akan diperoleh persamaan sebagai berikut ;
1212×OF×HP = 1212×FH×OQ
OF × HP = FH × OQ
2√6 × HP = 4√2 × 4
⇒ HP = 8383√3
HP = 2323 × HB
HP = 2323 × a√3
HP = 2323 × 4√3
HP = 8383√3
Jawaban : D
7. UN 2013
Kubus ABCD.EFGH memiliki panjang rusuk 6 cm. Jarak titik B ke CE adalah ...
A.  1212√3  cm
B.  1212√6  cm
C.  3√3  cm
D.  2√6  cm
E.  4√6  cm
Pembahasan :

Jarak B ke CE adalah BP
a = 6
BC = a = 6
BE = a√2 = 6√2
CE = a√3 = 6√3
Perhatikan Δ BCE siku-siku di B

BP = BC×BECEBC×BECE
BP = 6×6√26√36×6263
BP = 2√6

Jawaban : D
8. UN 2014
Diketahui limas beraturan T.ABCD dengan ABCD adalah persegi yang memiliki panjang AB = 4 dan TA = 6 cm. Jarak titik C ke garis AT = ...
A.  114114√14  cm
B.  2323√14  cm
C.  3434√14  cm
D.  4343√14  cm
E.  3232√14  cm
Pembahasan :

Jarak C ke AT adalah CP
AT = CT = 6
AC = 4√2
Perhatikan  Δ ACT

AP = AT2+AC2−CT22×ATAT2+AC2−CT22×AT
AP = 62+(4√2)2−622×662+(42)2−622×6
AP = 8383
Perhatikan Δ APC siku-siku di P
CP = √AC2−AP2AC2−AP2
CP = √(4√2)2−(83)2(42)2−(83)2
CP = 43√144314
Jawaban : D
9. UN 2004
Panjang rusuk kubus ABCD.EFGH adalah 6 cm. Jika S adalah titik potong EG dan FH, maka jarak DH ke AS adalah ... cm.
A.  2√3
B.  4
C.  3√2
D.  2√6
E.  6
Pembahasan :

Jarak DH ke AS adalah HS, karena HS tegak lurus terhadap DH dan AS.
rusuk = a = 6
HF = a√2 = 6√2
HS = 1212. HF
HS = 1212. 6√2
HS = 3√2

Jawaban : C

10. UN 2007
Diketahui sebuah kubus ABCD. EFGH. Besar sudut yang dibentuk oleh garis BG dengan BDHF adalah ...
A.  90°
B.  60°
C.  45°
D.  30°
E.  15°
Pembahasan :

Misalkan sudut yang dibentuk oleh BG dengan BDHF adalah β.
rusuk = a
BG = EG = a√2
PG = 1212 × EG = a2a2√2
Perhatikan Δ BPG siku-siku di P
sin β = PGBGPGBG = a2√2a√2a22a2 = 1212
Karena sin β = 1212, maka β = 30°

Jawaban : D

11. UN 2008
Diketahui kubus dengan panjang rusuk 6 cm. Jika sudut antara diagonal AG dengan bidang alas ABCD adalah α, maka sin α adalah ...
A. 1212√3
B. 1212√2
C. 1313√3
D. 1212E. 1313√2
Pembahasan :

Sudut antara AG dengan bidang alas ABCD adalah α.
rusuk = a = 6
CG = a = 6
AG = a√3 = 6√3
Perhatikan Δ ACG siku-siku di C
sin α = CGAGCGAG = 66√3663 = 1313√3
Jawaban : C

12. UN 2009
Balok ABCD. EFGH dengan panjang AB = BC = 3 cm dan AE = 5 cm. P terletak pada AD sehingga AP : PD = 1 : 2 dan Q terletak pada EG sehingga FQ : QG = 2 : 1. Jika α adalah sudut antara PQ dengan ABCD, maka tan α adalah ...
A. 1212√5
B. 110110√10
C. 1212√10
D. 1717√14
E. 1717√35
Pembahasan :

Sudut antara PQ dengan ABCD adalah α.
QR = 5
PS = 3
BS = SR = RC = 1
PR = √PS2+SR2=√32+12PS2+SR2=32+12
PR = √1010
Perhatikan Δ PQR siku-siku di R
tan α = QRPRQRPR = 5√10510 = 12√101210

Jawaban : C
13. UN 2012
Diketahui limas segi empat beraturan P.QRST, dengan rusuk alas 3 cm dan rusuk tegak 3√2 cm. Tangan sudut antara garis PT dan alas QRST adalah ...
A. 1313√3
B. √2
C. √3
D. 2√2
E. 2√3

Pembahasan :

Misalkan sudut antara garis PT dan alas QRST adalah θ.
QR = RS = ST = QT = 3
PQ = PR = PS = PT = 3√2
RT = a√2 = 3√2
Perhatikan bahwa PRT adalah segitiga sama sisi karena
PR = RT = PT = 3√2
sehingga θ = 60°
tan θ = tan 60° = √3
Jawaban : C
14. UN 2013
Pada kubus ABCD. EFGH sudut θ adalah sudut antara bidang BDE dengan bidang ABCD. Nilai dari sin θ adalah ...
A. 1414√3
B. 1212√3
C. 1313√6
D. 1212√2
E. 1313√3
Pembahasan :

Sudut antara bidang BDE dengan bidang ABCD adalah θ.
misalkan rusuk = a
AE = a
EO = a2a2√6
Perhatikan Δ AOE siku-siku di A
sin θ = AEEOAEEO =aa2√6aa26 = 2√626 = 1313√6
Jawaban : C
15. UN 2014
Kubus ABCD.EFGH memiliki rusuk 4 cm. Sudut antara AE dan bidang AFH adalah α. Nilai sin α adalah ...
A. 1212√2
B. 1212√3
C. 1313√3
D. 2323√2
E. 3434√3
Pembahasan :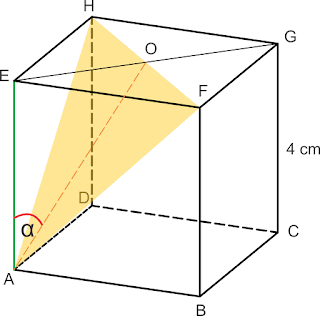

Sudut antara AE dan bidang AFH adalah α
rusuk = a = 4
EG = a√2 = 4√2
EO = 1212 × EG = 2√2
AO = a2a2√6 = 2√6
Perhatikan Δ AEO siku-siku di E
sin α = EOAOEOAO = 2√22√6=√2√62226=26 = 1313√3

Jawaban : C

16. UN 2007
Diketahui bidang 4 beraturan ABCD dengan panjang rusuk 8 cm. Kosinus sudut antara bidang ABC dan bidang ABD adalah ...
A. 1313

B. 1212
C. 1313√3
D. 2323
E. 1212√3
Pembahasan :

Misalkan sudut antara bidang ABC dan ABD adalah θ.
Karena bangun diatas merupakan bidang empat beraturan, pastilah ke-4 bidangnya merupakan segitiga sama sisi.
rusuk (a) = 8
DC = a = 8
PC = PD = a2a2√3 = 4√3
Perhatikan Δ PCD, dengan aturan cosinus diperoleh :
cos θ = PC2+PD2−DC22×PC×PDPC2+PD2−DC22×PC×PD
cos θ = (4√3)2+(4√3)2−822×4√3×4√3(43)2+(43)2−822×43×43
cos θ = 1313

Jawaban : A
17. UN 2015
Kubus ABCD. EFGH dengan rusuk 12 cm, tangen sudut antara bidang AFH dengan bidang CFH adalah...
A. 1313
B. 1212√2
C. 2323√2
D. √2
E. 2√2
Pembahasan :

Misalkan sudut antara bidang AFH dan CFH adalah θ.
Perhatikan segitiga ACP
AP = CP = a2a2√6 = 122122√6 = 6√6
AC = a√2 = 12√2
Dengan aturan cosinus
Cos θ = AP2+CP2−AC22.AP.CPAP2+CP2−AC22.AP.CP
Cos θ = (6√6)2+(6√6)2−(12√2)22.6√6.6√6(66)2+(66)2−(122)22.66.66
Cos θ = 216+216−288432216+216−288432
Cos θ = 1313
Cos θ = 1313
sisi samping = 1
sisi miring = 3
sisi depan = √32−1232−12 = √8 = 2√2
tan θ = depansampingdepansamping = 2√21221 = 2√2
Jadi, tangen sudut antara bidang AFH dan CFH adalah 2√2.
Jawaban : E

18. UN 2015
Diketahui kubus ABCD. EFGH dengan panjang rusuk 4 cm. Titik M adalah titik tengah AB. Jarak titik E ke CM sama dengan...
A. 4545√30 cm
B. 2323√30 cm
C. 2√5 cm
D. 2√3 cm
E. 2√2 cm
Pembahasan :

CM = EM = a2a2√5 = 4242√5 = 2√5
CE = a√3 = 4√3
MN = a√2 = 4√2
Karena MN dan CE berpotongan tegak lurus dan sama besar di titik Q, maka
MQ = 1212×MN = 2√2
Perhatikan segitiga CEM, ∠M adalah sudut tumpul karena CE2 > CM2 + EM2, sehingga jarak titik E ke CM adalah jarak dari titik E ke perpanjangan CM yaitu EP.
Dengan menggunakan rumus luas segitiga pada segitiga CEM akan diperoleh persamaan sebagai berikut :
1212×CM×EP = 1212×CE×MQ
CM × EP = CE × MQ
2√5 × EP = 4√3 × 2√2 (kali √5)
10 × EP = 8√30
EP = 4545√30
Jawaban : A
RALAT : 10/8/2017
Yang ditanyakan adalah jarak titik E ke CM, bukan jarak titik E ke perpanjangan CM.
CM adalah ruas garis, dengan titik-titik ujungnya C dan M. Jadi, jarak titik E ke CM adalah jarak terdekat dari titik E ke ruas garis CM, yaitu EM = 2√5 (C)

19. UN 2016
Diketahui kubus ABCD EFGH dengan panjang rusuk 8 cm. Jarak titik E ke garis FD adalah...
A. 8383√2 cm
B. 8383√3 cm
C. 8383√6 cm
D. 103103√6 cm
E. 4√6 cm
Pembahasan :

Jarak titik E ke garis FD adalah EP.

Perhatikan segitiga DEF siku-siku di E
EF = 8
DE = 8√2
DF = 8√3

EP = DE×EFDFDE×EFDF
EP = 8√2×88√382×883
EP = 8383√6

Jawaban : C
20. UN 2016
Diketahui kubus ABCD EFGH dengan AB = 16 cm. Nilai sinus sudut antara garis AH dengan bidang BDHF adalah...
A. 1212
B. 1313√3
C. 1212√2
D. 1212√3
E. 1313√6
Pembahasan :

Misalkan sudut yang dibentuk oleh AH dengan BDHF adalah θ.
rusuk = a = 16 cm
AH = AC = a√2 = 16√2
AP = 1212×AC = 8√2
Perhatikan Δ AHP siku-siku di P
sin θ = APAHAPAH = 8√216√282162 = 1212

Jawaban : A

UPDATE 21/10/17

Untuk Ujian Nasional matematika IPA tahun 2017, materi dimensi tiga dikeluarkan sebanyak 4 soal dalam satu paket.
21. UN 2017
Diketahui kubus ABCD.EFGH dengan panjang rusuknya 6 cm. Jika α adalah sudut antara bidang AFH dan bidang BDHF, nilai sin α = ...
A.  1/2
B.  1/3 √3
C.  1/2 √2
D.  1/2 √3
E.  2/3 √2
Pembahasan :

AC = a√2 = 6√2
AP =  1212. AC = 3√2
AO = a2a2√6 = 3√6
Perhatikan segitiga AOP siku-siku di P.
sin α = APAOAPAO = 3√23√63236 = 1313√3
Jawaban : B
22. UN 2017
Diketahui kubus KLMN.OPQR dengan panjang rusuknya 6 cm. Jarak titik M ke bidang LNQ adalah ...
A.  2√2  cm
B.  2√3  cm
C.  3√2  cm
D.  3√3  cm
E.  4√3  cm
Pembahasan :
Jarak M ke LNQ = jarak M ke QS, yaitu MT.

SM = 1212. KM = 3√2
MQ = 6
SQ = a2a2√6 = 3√6
Perhatikan segitiga SMQ siku-siku di M. Pada segitiga siku-siku, jarak dari titik sudut siku-siku ke sisi miringnya adalah hasil kali dari kedua sisi siku-siku dibagi sisi miring.
Jadi, MT = SM⋅MQSQSM⋅MQSQ = 6⋅3√23√66⋅3236 = 2√3
atau
MT = 1313. MO = 1313. 6√3 = 2√3
Jawaban : B
23. UN 2017
Diketahui limas beraturan T.ABCD. Panjang rusuk tegak dan panjang rusuk alas 4 cm. Jarak titik A ke TB adalah ...
A.  2√2  cm
B.  2√3  cm
C.  4  cm
D.  4√2  cm
E.  4√3  cm
Pembahasan :
Jadi, jarak titik A ke TB adalah AP.

Perhatikan segitiga sama sisi ABT dengan panjang sisinya 4 cm. Pada segitiga sama sisi yang panjang sisinya a, jarak dari titik sudut ke sisi di depannya adalah a2a2√3.
Jadi, jarak titik A ke TB adalah
AP = 4242√3 = 2√3
Jawaban : B
24. UN 2017
Diketahui limas beraturan T.ABCD dengan panjang rusuk tegak 6√2 cm dan panjang rusuk alas 6 cm. Jarak titik A ke TC adalah ...
A.  2√2  cm
B.  2√3  cm
C.  3√2  cm
D.  3√3  cm
E.  3√6  cm
Pembahasan :
Jarak titik A ke TC adalah AP.

AC = a√2 = 6√2
Karena AC = TC = AT, maka ACT adalah segitiga sama sisi dengan panjang sisi 6√2.
Jadi, AP = 6√22622√3 = 3√6
Jawaban : E
25. UN 2017
Diketahui limas alas segiempat beraturan T.ABCD. Panjang rusuk tegak = rusuk alas = 4 cm. Sudut antara garis TA dan bidang alas ABCD adalah ...
A.  15°
B.  30°
C.  45°
D.  60°
E.  90°
Pembahasan :
Misalkan sudut antara garis TA dan bidang alas ABCD adalah α.

AC = 4√2
AO = 1212. AC = 2√2
AT = 4
Perhatikan segitiga AOT siku-siku di O.
cos α = AOATAOAT = 2√24224 = 1212√2
Karena cos α = 1212√2 maka α = 45°
Jawaban : C
26. UN 2017
Diketahui limas segienam beraturan T.ABCDEF rusuk alasnya 6 cm dan tinggi limas 6√3 cm. Nilai sinus sudut antara rusuk tegak dan bidang alas limas adalah ...
A.  1/3 √2
B.  1/2
C.  1/3 √3
D.  1/2 √2
E.  1/2 √3
Pembahasan :
Misalkan sudut antara rusuk tegak dengan bidang alas adalah α.

Perhatikan segitiga COT siku-siku di O.
CT = √(CO)2+(OT)2(CO)2+(OT)2
CT = √(6)2+(6√3)2(6)2+(63)2
CT = 12
sin α = OTCTOTCT = 6√3126312 = 1212√3
atau
tan α = OTCOOTCO = 6√36636 = √3
Karena tan α = √3, maka α = 60°
Jadi, sin α = sin 60° = 1212√3
Jawaban : E

27. UN 2017
Diketahui kubus ABCD.EFGH, panjang rusuknya 12 cm dan α adalah sudut antara bidang BDG dan ABCD. Nila sin α adalah ...
A.  1/6 √6
B.  1/3 √3
C.  1/2 √2
D.  1/3 √6
E.  1/2 √3
Pembahasan :

CG = a = 12
OG = a2a2√6 = 6√6
Perhatikan segitiga OCG siku-siku di C.
sin α = CGOGCGOG = 126√61266 = 1313√6

Jawaban : D