INTI ATOM DAN RADIOAKTIVITAS
I. PILIHAN GANDA
Pilihlah jawaban yang
tepat. Berikan alasan mengapa Anda memilih jawaban tersebut. Jika diperlukan
gunakan konstanta g = 10 m/s2, c = 3 x 108 m/s,
e = 1,6 x 10-19 C, me = 9,1 x 10-31 kg,
h = 6,6 x 10-34 Js, u = 1 sma = 931 MeV.
1.
Pernyataan berikut yang
merupakan teori atom menurut Dalton adalah …
a.
Bagian terkecil dari
suatu atom adalah elektron
b.
Elektron dari suatu
unsur sama dengan elektron unsur lain
c.
Sebagian besar massa
atom terkumpul pada intinya
d.
Atom dari suatu unsur
tidak dapat bergabung dengan atom unsur lain
e.
Atom dari unsur-unsur
yang sama mempunyai sifat sama pula
Jawaban :
Jawaban : E
Diketahui :
Teori atom Dalton
Ditanyakan :
Pernyataan yang benar =
..?
Jawaban :
John Dalton adalah seorang ilmuwan Inggris, pada tahun 1803 ia membuktikan
konsep atom Demokritus secara empirik berdasarkan eksperimen. Model atom yang
dikemukakan Dalton adalah:
·
- Atom adalah bagian terkecil
dari suatu zat yang tidak dapat dibagi lagi.
- Atom-atom suatu unsur semuanya
serupa dan tidak dapat berubah menjadi atom unsur lain. Misalnya, atom
perak tidak dapat berubah menjadi atom besi.
- Dua atom atau lebih dari
unsur-unsur berlainan dapat membentuk suatu molekul.
Misalnya, atom hidrogen dan atom oksigen bersenyawa membentuk molekul air
(H2O).
- Pada suatu reaksi kimia,
atom-atom berpisah kemudian bergabung lagi dengan susunan yang berbeda
dengan semula tetapi massanya tetap.
- Beberapa atom dapat bergabung
menurut perbandingan tertentu yang sederhana.
Keunggulan teori atom Dalton yaitu dilandasi fakta-fakta dan
temuan eksperimen berdasarkan hukum massa (Lavoisier) dan hukum perbandingan
tetap (Proust).
2.
Pernyataan berikut yang
tepat menggambarkan nilai perbandingan muatan dan massa sinar katode yang
diperoleh Thompson adalah …
a.
Bergantung pada jenis
gas dalam tabung
b.
Bergantung pada jenis
bahan elektrode
c.
Bergantung pada jenis
bahan tabung
d.
Bergantung pada tegangan
pemercepat
e.
Lebih besar daripada
nilai yang diperoleh pada proton
Jawaban :
Jawaban : D
Diketahui :
Teori Thomson
Ditanyakan :
Pernyataan yang benar
=…?
Pada penelitiannya, Thompson melewatkan arus melalui tabung sinar
katoda (Gambar di samping). Sebuah tabungsinar katoda adalah tabung gelas yang hampir semua udara
telah dihilangkan. Ini berisi sepotong logam (elektroda) pada setiap ujungnya.
Satu elektroda bermuatan negatif disebut katoda, dan elektroda lainnya yang
bermuatan positif disebut anoda. Ketika tegangan tinggi arus listrik diterapkan
pada ujung plat, sinar katoda berjalan dari katoda ke anoda. Sinar katoda ini
disebut elektron. Thompson juga mengukur massa partikel yang telah
diidentifikasi. Dia melakukan ini dengan menentukan berapa banyak sinar katoda
yang membelok ketika ia meberi variasi tegangan. Ia menemukan bahwa massa
partikel adalah 2000 kali lebih kecil dari massa atom terkecil, yakni atom
hidrogen. Singkatnya, Thompson telah menemukan keberadaan partikel yang lebih
kecil dari atom yaitu elektron.
3.
Dalam eksperimen
Rutherford, sejumlah partikel alfa yang mulanya ditembakkan ke lempeng tipis
emas, ternyata sebagian kecilnya dihamburkan pada sudut besar. Hamburan ini
terjadi karena partikel alfa …
1.
a.
Menumbuk partikel berat
bermuatan negatif yang tersebar pada seluruh lempeng emas.
b.
Ditolak oleh partikel
berat bermuatan positif yang tersebar pada seluruh lempeng emas.
c.
Menumbuk partikel berat
bermuatan negatif yang terkonsentrasi pada daerah kecil lempeng emas.
d.
Ditolak oleh partikel
berat bermuatan positif yang terkonsentrasi pada daerah kecil lempeng emas.
e.
Bertumbukan dengan
partikel alfa yang lain.
Jawaban :
Jawaban : D
Diketahui :
Teori Rutherford
Ditanyakan :
Pernyataan yang benar
=…?
Jawaban :
Ernest Rutherford beserta dua orang asistennya, Geiger dan Marsden melakukan
percobaan apda tahun 1911. Teknik yang digunakan dalam percobaannya adalah
seperti pada gambar di samping. Seberkas partikel alfa (α) ditembakkan melalui
celah pelat timbel dan akhirnya menumbuk lempeng emas. Untuk mendeteksi partikel
α yang keluar dari lempeng emas, dipasang lempeng yang berlapis seng
sulfida. Jika partikel α menumbuk lempeng ini, akan tampak suatu nyala
sekilas yang dapat diamati secara visual. Hasilnya adalah sebagian besar
partikel α lewat tanpa mengalami pembelokan/hambatan, sebagain kecil
dibelokkan, dan sedikit sekali yang dipantulkan kembali. kemudian, Rutherfoard
menyatakan tiga kesimpulan sebagai berikut:
·
- Sebagian besar partikel α
menembus lempeng logam tanpa dibelokkan. Peristiwa ini menunjukkan bahwa
sebagian besar ruang dalam atom-atom emas adalah ruang kosong.
- Sedikit sekali partikel α yang
dipantulkan kembali. Peristiwa ini menunjukkan bahwa partikel telah
menumbuk bagian yang sangat keras dari atom, yang disebut inti
atom. Bagian ini mempunyai ukuran sangat kecil dibandingkan dengan
ukuran atomnya.
- Sebagian partikel α Peristiwa
ini menunjukkan bahwa muatan inti atom adalah sejenis dengan muatan
partikel α (positif). Partikel α yang lewat dekat inti atom dibelokkan
oleh gaya tolak-menolak muatan-muatan listrik yang sejenis.
4.
Dalam model atomnya,
Bohr menganggap bahwa elektron-elektron …
1.
a.
Didistribusikan secara
seragam dalam keseluruhan atom
b.
Dilokasikan hanya dalam
inti atom
c.
Dilokasikan hanya dalam
sejumlah orbit-orbit tertentu
d.
Memancarkan cahaya ketika
beredar dalam orbitnya
e.
Memancarkan cahaya
ketika berpindah dari orbit dalam ke orbit luar
Jawaban :
Jawaban : E
Diketahui :
Teori atom Bohr
Ditanyakan :
Pernyataan yang benar
=…?
Jawab :
Model Atom Bohr dinyatakan oleh 4 kesimpulan berikut:
·
- Elektron bergerak dalam
orbit-orbit melingkar di sekitar proton di bawah pengaruh gaya Coulomb.
- Elektron tidak dapat berputar
di sekitar inti melalui setiap orbit, tetapi elektron hanya melalui
orbit-orbit tertentu tanpa meradiasikan energi. Orbit stabil ini
disebut orbit stasioner yang memiliki energi tertentu
yang tetap, dan karena itu fisika klasik boleh digunakan untuk
menjelaskan gerak elektron pada orbit-orbit stasioner ini.
- Radiasi dipancarkan oleh atom
ketika elektron “melompat” dari suatu keadaan stasioner (orbit stasioner)
yang energinya lebih tinggi ke keadaan stasioner lain yang energinya
lebih rendah.
- Ukuran dari orbit-orbit
diperkenankan ditentukan oleh kuantum tambahan, yaitu momentum sudut
orbital elektron.
5.
Garis-garis spektrum
Paschen dihasilkan jika dalam atom hidrogen terjadi transisi elektron dari
tingkat yang lebih tinggi ke tingkat n = 3. Jika tetapan
Rydberg 1,097 x 107 m-1, panjang gelombang
terpendek dari deret Paschen adalah …
1.
a.
8,2 x 10-7 m
b.
11,3 x 10-7 m
c.
14,4 x 10-7 m
d.
16,7 x 10-7 m
e.
18,8 x 10-7 m
Jawaban :
Jawaban : A
Diketahui :
n = 3
R = 1,097 x 107 m-1
Ditanyakan :
λterpendek dari
deret Paschen =…?
Jawaban :
Secara umum, rumus deret
dapat dinyatakan sebagai berikut:
1λ=R(1n2−1m2)
dengan n<m dan m
=(n+1)(n+2)…
Untuk deret Paschen,n =
3 dan m = 4,5,6 ,…. Karena ditanyakan panjang gelombang
terpendek maka m = ∞ (berbanding terbalik dengan panjang
gelombang). Maka:
1λ=1,097×107m−1(132−1∞2)1λ=1,097×107m−1×19λ=91,097×107λ=8,2×10−7m
6.
Jika konstanta Rydberd
1,097 x 107 m-1, panjang gelombang terpendek
pada deret Balmer adalah … (dalam angstrom)
1.
a.
6,563
b.
6.352
c.
5.678
d.
3.646
e.
3.464
Jawaban :
Jawaban : D
Diketahui :
R = 1,097 x 107 m-1
Ditanyakan :
λterpendek dari
deret Balmer (Angstrom) =…?
Jawaban :
Secara umum, rumus deret
dapat dinyatakan sebagai berikut:
1λ=R(1n2−1m2)
dengan n < m dan m = (n + 1)(n + 2),…
Untuk deret Paschen,n =
3 dan m = 4,5,6 ,…. Karena ditanyakan panjang gelombang
terpendek maka m = ∞ (berbanding terbalik dengan panjang
gelombang). Maka:
1λ=1,097×107m−1(122−1∞2)1λ=1,097×107m−1×14λ=41,097×107λ=3,64×10−7mλ=3646A˚
7.
Keberadaan tingkat
energi di dalam atom dapat ditunjukkan secara langsung dengan mengamati bahwa …
1.
a.
Atom dapat memancarkan
spektrum garis
b.
Fotoelektron hanya dapat
dipancarkan dari permukaan logam ketika cahaya yang menyinari memiliki panjang
gelombang kritis
c.
Partikel dipantulkan
balik dengan sudut besar oleh atom-atom dalam zat padat
d.
Sinar-X terhambur apabila
mengenai padatan kristal
e.
Atom-atom di dalam zat
padat mendifraksikan elektron seperti pada gejala difraksi sinar-X oleh kristal
Jawaban :
Jawaban : A
Diketahui :
Keberadaaan tingkat
energi atom
Ditanyakan :
Pernyataan yang benar =
..?
Jawaban :
Keberadaan tingkat
energi pada atom dapat ditunjukkan dengan kemampuan suatu atom untuk
memancarkan spektrum garis.
8.
Sebuah karbon memiliki
nomor massa 12 dan nomor atom 6.
1.
i.
Lambangnya adalah 126C
ii.
Mengandung 6 proton, 6
neutron, dan 6 elektron
iii.
Satu dari isotopnya
memiliki 6 proton, 7 neutron, dan 6 elektron
Pernyataan yang benar adalah pernyataan nomor …
1.
a.
(i), (ii), dan (iii)
b.
(i) dan (ii)
c.
(ii) dan (iii)
d.
(i)
e.
(iii)
Jawaban :
Jawaban : A
Diketahui :
Karbon memiliki nomor
massa 12 dan nomor atom 6
Ditanyakan :
Pernyataan yang benar
=….?
Jawaban :
Jumlah proton dalam suatu inti atom disebut nomor atom,
dilambangkan oleh Z. Adapun jumlah nukleon (proton dan neutron)
dalam inti atom disebut nomor massa, dilambangkan oleh A. Jika
unsur dilambangkan oleh X, inti atom dengan nomor atom dan nomor massa tertentu
disebut nuklida. Sebuah nuklida dilambangkan sebagai berikut:
AZX
Dengan begitu dapat
ditentukan jumlah proton, elektron dan neutron sebagai berikut:
Jumlah proton = Z
Jumlah neutron = A – Z
Jumlah elektron = Z
(untuk atom netral)
Maka untuk karbon yang mempunyai lambang C ditulis dengan 126Cdan proton = 6, neutron = 12 – 6 = 6 , serta elektron = 6 .
Isotop didefinisikan
sebagai nuklida-nuklida dengan jumlah proton sama tetapi jumlah neutron
berbeda. Isobar didefinisikan sebagai nuklida-nuklida dengan
jumlah neuklon sama, tetapi jumlah proton berbeda. Sedangkan isoton didefinisikan
sebagai nuklida-nuklida dengan jumlah neutron yang sama. Dengan demikian isotop
dari karbon harus memiliki proton 6 tetapi neutronnya berbeda.
9.
Suatu atom X mempunyai
21 proton, 21 elektron, dan 34 neutron. Simbol untuk atom ini adalah …
1.
a.
7642X
b.
7621X
c.
5542X
d.
5521X
e.
3421X
Jawaban :
Jawaban : D
Diketahui :
Atom X mempunyai 21
proton, 21 elektron, dan 34 neutron
Ditanyakan :
Simbol atom =…?
Jawaban :
Jumlah proton dalam suatu inti atom disebut nomor atom,
dilambangkan oleh Z. Adapun jumlah nukleon (proton dan neutron)
dalam inti atom disebut nomor massa, dilambangkan oleh A. Jika
unsur dilambangkan oleh X, inti atom dengan nomor atom dan nomor massa tertentu
disebut nuklida. Sebuah nuklida dilambangkan sebagai berikut:
AZX
Dengan begitu dapat
ditentukan jumlah proton, elektron dan neutron sebagai berikut:
Jumlah proton = Z
Jumlah neutron = A – Z
Jumlah elektron = Z
(untuk atom netral)
Maka untuk karbon yang mempunyai lambang X ditulis dengan Z =
proton dan elektron = 21 sedangkan sehingga A =
neutron + Z = 34 +21= 55 sehingga 5521X.
10. Semua isotop oksigen memiliki … yang sama.
1.
a.
Nomor atom
b.
Muatan nuklir
c.
Sifat-sifat fisika
d.
Waktu paro
e.
Rasio muatan terhadap
massa
Jawaban :
Jawaban : A
Diketahui :
Isotop oksigen
Ditanyakan :
Pilihan yang benar =…?
Jawaban :
Isotop didefinisikan
sebagai nuklida-nuklida dengan jumlah proton sama tetapi jumlah neutron berbeda. Isobar didefinisikan
sebagai nuklida-nuklida dengan jumlah neuklon sama, tetapi jumlah proton
berbeda. Sedangkan isoton didefinisikan sebagai
nuklida-nuklida dengan jumlah neutron yang sama. Dengan demikian isotop dari
oksigen memiliki proton yang sama, dimana proton = Z = nomor atom.
11. Energi ikat inti adalah energi yang …
1.
a.
Diperlukan untuk
menyatukan proton-proton dan neutron-neutron dalam inti atom
b.
Diperlukan untuk
memutuskan inti atom menjadi proton-proton dan neutron-neutron
c.
Diperlukan untuk
menyatukan proton-proton, neutron-neutron, dan elektron-elektron dalam sebuah
atom
d.
Dibebaskan ketika
proton-proton dan neutron-neutron bersatu dalam inti atom
e.
Dibebaskan ketika inti
atom pecah menjadi proton-proton dan neutron-neutron
Jawaban :
Jawaban : B
Diketahui :
Energi ikat
Ditanyakan :
Pernyataan yang benar
=..?
Jawaban :
Gaya-gaya inti kuat mengikat nukleon-nukleon untuk bersatu dalam
sebuah inti stabil. Oleh karena itu, diperlukan energi untuk memisahkan sebuah
inti stabil menjadi proton-proton dan neutron-neutron pembentuknya. Semakin
stabil sebuah inti, semakin besar energi yang diperlukan untuk memutuskan inti
tersebut menjadi proton-proton dan neutron-neutron pembentuknya. Energi
yang diperlukan untuk memutuskan inti menjadi proton-proton neutron-neutron
pembentuknya disebut energi ikat inti (binding energy).
12. Jika massa deuteron 2,014 sma, massa
proton 1,008 sma, massa neutron 1,009 sma, energi ikat
deuteron adalah … MeV
1.
a.
2,793
b.
9,31
c.
27,93
d.
93,1
e.
279,3
Jawaban :
Jawaban : A
Diketahui :
md = 2,014 sma
mp = 1,008 sma
mn = 1,009 sma
Ditanyakan :
Edeutron (MeV)
=…?
Jawaban :
Deuteron adalah atom yang memiliki 1 neutron dan 1 proton pada
intinya, atau nomor massa (A) 2 dan nomor atom (Z) 1. Untuk mengetahui energi
ikat deuteron adalah …
E=Δm×931MeVE=[(Zmp+(A−Z)mn)−md]×931MeVE=[((1×1,008)+(1×1,009))−2,014]×931E=[(1,008+1,009)−2,014]×931E=[2,017−2,014]×931E=2,793MeV
13. Hasil peluruhan radioaktif yang tidak dapat
disimpangkan oleh medan magnetik adalah …
1.
a.
Partikel alfa
b.
Sinar gamma
c.
Sinar gamma dan partikel
beta
d.
Partikel alfa dan
partikel beta
e.
Sinar gamma dan partikel
alfa
Jawaban :
Jawaban : B
Diketahui :
Hasil peluruhan
radioaktif yang tidak dapat disimpangkan oleh medan magnetik
Ditanyakan :
Pernyataan yang benar
=..?
Jawaban :
Sifat-sifat sinar α, β,
dan γ dapat dilihat pada tabel berikut ini:
14. Perhatikan pernyataan-pernyataan berikut :
1.
i.
Tidak bermuatan listrik.
ii.
Bermuatan listrik
iii.
Mendapat gaya magnetik
yang berfungsi sebagai gaya sentripetal.
iv.
Mendapat gaya
sentripetal yang berfungsi sebagai gaya magnetik.
Pernyataan yang merupakan penyebab sinar membentuk lintasan
lingkaran jika memasuki medan magnetik homogen secara tegak lurus ditunjukkan
oleh nomor …
1.
a.
(i) dan (ii)
b.
(i) dan (iii)
c.
(ii) dan (iii)
d.
(ii) dan (iv)
e.
(iii) dan (iv)
Jawaban :
Jawaban : C
Diketahui :
Pernyataan yang
merupakan penyebab sinar membentuk lintasan lingkaran jika memasuki medan
magnetik homogen secara tegak lurus
Ditanyakan :
Pernyataan yang benar
=..?
Jawaban :
Pada tahun 1899, Ernest Rutherford melakukan
percobaan dalam rangka studinya mengenai radioaktif. Ia menempatkan sedikit radium di dasar sebuah kotak kecil dari timah
hitam (timbel). Ia memerhatikan sinar-sinar yang dipancarkan dari kotak karena
adanya pengaruh sebuah medan magnetik kuat yang berarah tegak lurus terhadap
arah rambat radiasi ketiga sinar yang dipancarkan oleh radium. Dia mendapatkan
bahwa berkas sinar terpisah menjadi tiga komponen, seperti pada
gambar di samping. Dengan memerhatikan arah sinar yang dibelokkan dia
menyimpulkan bahwa komponen sinar yang tidak dibelokkan adalah tidak
bermuatan (sinar γ), komponen sinar yang dibelokkan ke kiri adalah
bermuatan negatif (sinar β), dan yang dibelokkan ke kanan adalah
bermuatan positif (sinar α). Dengan menggunakan konsep gaya
Lorentz:
FL= BQV
sinθ ( θ=90o)
Arahnya menuju ke pusat lingkaran sehingga berfungsi sebagai gaya
sentripetal.
15.
Radiasi X, Y, dan Z dari
gambar berikut adalah …
1.
a.
X = Alfa,Y = Beta, Z =
Gamma
b.
X = Alfa,Y = Gamma, Z =
Beta
c.
X = Gamma,Y = Alfa, Z =
Beta
d.
X = Gamma,Y = Beta, Z =
Alfa
e.
X = Beta,Y = Gamma, Z =
Alfa
Jawaban :
Jawaban : B/E
Diketahui :
Radiasi X, Y, dan Z
Ditanyakan :
Sinar yang benar =…?
Jawaban :
Urutan daya tembus sinar
radioaktif dari yang terkecil ke yang terbesar adalah α,β,γ. Secara
singkat urutan daya tembus adalah sebagai berikut:
sinar α < sinar β
< sinar γ
16. Pada proses peluruhan 21581Bi menjadi 21584Po terjadi pelepasan tiga buah …
1.
a.
Positron
b.
Partikel α
c.
Neutron
d.
Proton
e.
Elektron
Jawaban :
Jawaban : E
Diketahui :
Proses peluruhan
Ditanyakan :
Yang dilepaskan =…?
Jawaban :
Peluruhan radioaktif
dapat dilihat berdasarkan tabel dibawah ini:
Pada proses peluruhan 21581Bi menjadi 21584Po terjadi perubahan nomor atom dari 81
menjadi 84 yang mana berubah menjadi +3. Ini proses peluruhan merupakan
pemancaran elektron.
17.
Pada proses peluruhan 23892Umenjadi 23490Thterjadi pelepasan satu
buah …
1.
a.
Partikel Alfa
b.
Partikel beta
c.
Partikel gamma
d.
Neutron
e.
Positron
Jawaban ;
Jawaban : A
Diketahui :
Proses peluruhan
Ditanyakan :
Yang dilepaskan =…?
Jawaban :
Peluruhan radioaktif
dapat dilihat berdasarkan tabel dibawah ini:
Pada proses peluruhan 23892U menjadi 23490Th terjadi perubahan
massa atom yaitu -4 dan perubahan nomor atom -2. Maka proses peluruhan ini
merupakan pelepasan satu buah partikel alfa.
18. Hubungan antara waktu paro (τ) dan tetapan
peluruhan (λ) adalah …
1.
a.
τ = ln2
b.
τ = λ
c.
τ=ln2λ
d.
τ = λ ln2
e.
τ=1λ
Jawaban :
Jawaban : C
Diketahui :
Waktu paro (τ) dan
tetapan peluruhan (λ)
Ditanyakan :
Hubungan antara waktu
paro (τ) dan tetapan peluruhan (λ) =…?
Jawaban :
Waktu paro dari suatu isotop radioaktif adalah selang waktu yang dibutuhkan
agar aktivitas radiasi berkurang setengah dari aktivitas semula atau selang
waktu yang dibutuhkan agar setengah dari inti radioaktif yang ada meluruh.
Hubungan antara waktu paro (τ) dan tetapan peluruhan ( λ) adalah :
τ=ln2λ
19. Berdasarkan grafik peluruhan berikut, jumlah zat radioaktif setelah meluruh selama 1 menit adalah …
1.
a.
164No
b.
112No
c.
16No
d.
12No
e.
6364No
Jawaban :
Jawaban : A
Diketahui :
Berdasarkan grafik di
samping dapat diidentifikasi bahwa:
N0 = N0
t = 1 menit = 60 s
T12=10
Ditanyakan :
N =…?
Jawaban :
N=N0(12)t/T12N=N0(12)6010N=N0(12)6N=164N0
20. Umur waktu paro Na-24 adalah 30 hari. Waktu yang
diperlukan agar 75% sampel yang mengandung nuklida ini meluruh adalah …
1.
a.
15 hari
b.
30 hari
c.
45 hari
d.
60 hari
e.
75 hari
Jawaban :
Jawaban : D
Diketahui :
NN0 = 1- 75% = 25% (sisa yang belum meluruh)
Ditanyakan :
t =…?
Jawaban :
N=N0(12)t/T12NN0=(12)t300,25=(12)t30(12)2=(12)t302=t30t=2×30t=60hari
21. Setelah 72 hari, I-131 yang memiliki paruh waktu
paro 8 hari tersisa sebanyak 4 g. Massa awal unsur tersebut adalah
…
1.
a.
80 g
b.
720 g
c.
2.048 g
d.
5.120 g
e.
8.260 g
Jawaban :
Jawaban : C
Diketahui :
m = 4 gram
T12=8hari
t = 72 hari
Ditanyakan :
m0 =..?
Jawaban :
m=m0=(12)tT12m0=m(12)tT12m0=4(12)728m0=4(12)9m0=4(1512)m0=4×512m0=2.048hari
22. Unsur 210Bi yang waktu paronya 5
hari meluruh menurut 210Bi -> 210Po
+ β . Jika mula-mula
terdapat 96 g unsur 210Bi, setelah 10 hari
akan dihasilkan 210Po sebanyak …
1.
a.
6 g
b.
24 g
c.
60 g
d.
72 g
e.
90 g
Jawaban ;
Jawaban : D
Diketahui :
mo = 96 gram
T12=5hari
t = 10 hari
Ditanyakan :
m =…?
Jawaban :
m=m0m=(12)tT12m=96(12)105m=96(12)2m=96⋅14m=24gram
Ini berarti massa 210Bi yang telah meluruh 210Po adalah:
mo – m = 96 – 24 = 72 gram
23. Dalam suatu batuan meteorit tertentu, nilai
perbandingan jumlah atom 23892Udan jumlah atom timbel
20682Pb akibat peluruhan
23892U adalah . Jika waktu
paro atom uranium adalah 6 x 109 tahun, perkiraan usia batuan
adalah …
1.
a.
1,5 x 109 tahun
b.
3 x 109 tahun
c.
6 x 109 tahun
d.
12 x 109 tahun
e.
18 x 109 tahun
Jawaban :
Jawaban : E
Diketahui :
23892U20692Pb=78T12U=6,0x109tahun
Ditanyakan :
Perkiraan usia =…?
Jawaban :
Ketika batuan mula-mula terbentuk, yang ada hanyalah radioisotope
U-238 sedang isotop stabil Pb-206. Jadi, jumlah atom U-238 yang meluruh
membentuk jumlah atom Pb-206. Dengan kata lain 23892U20692Pb=23892Uawal20692Pbakhir=78=peluruhan. Dan untuk mencari sisa uranium adalah:
NN0=1−78=18
Berdasarkan persamaan di
bawah ini :
N=N0(12)t/T1218=(12)t6,0×109(12)3=(12)t6,0×1093=t6,0×109t=3×(6,0×109)t=18×109
24. Dua unsur radioaktif X dan Y memiliki
waktu paro masing-masing 40 menit dan 50 menit. Jika sampel A dan B mula-mula
mengandung jumlah atom yang sama. Setelah 200 menit nilai perbandingan jumlahatomXyangbelummeluruhjumlahatomYyangbelummeluruh adalah …
1.
a.
4
b.
2
c.
1A
d.
12
e.
14
Jawaban :
Jawaban : D
Diketahui :
τX=40menitτY=50menitN0X=N0Yt=200menit
Ditanyakan :
NxNY=..?
Jawaban :
Secara umum, banyak inti
atom yang tersisa (belum meluruh) setelah selang waktu t=nT12 dapat ditentukan menggunakan persamaan
berikut:
N=N0(12)t/T12
NXNY=N0(12)tT12N0(12)tT12NXNY=(12)20040(12)20050NXNY=(12)5(12)4NXNY=132116NXNY=12
25. Jika tebal suatu bahan yang digunakan untuk
menahan intensitas radioaktif adalah sebesar 1 HVL, intensitas
sinar radioaktif yang dilewatkan adalah setengah dari intensitas semula. Jika
tebal bahan diubah menjadi 3 HVL, intensitas sinar yang dilewatkan
adalah …
1.
a.
50%
b.
25%
c.
15%
d.
12,5%
e.
6,25%
Jawaban :
Jawaban : D
Diketahui :
x1 = HVL -> I1 =
12
x2 =
3 HVL
Ditanyakan :
I2 = …I0
Jawaban :
Rumus lapisan harga paro, HVL, berkaitan intensitas sinar
radioaktif mirip seperti rumus waktu paro, T, yang berkaitan dengan aktivitas
radiasi yang tertinggal.
A=A0(12)ndengann=tTmiripdenganI=I0(12)ndengann=xHVL
Jika x1 =
1 -> I1 = 12, maka nilai I0 adalah
:
I1=I0(12)n12=I0(12)1HVL/HLI0=1
Dari nilai x yang telah
diketahui maka :
I2=I0(12)nI2=1(12)3HVLHVLI2=1(12)3I2=1(18)I2=12,5persen
26. Alat deteksi radioaktivitas yang mengubah
timbunan elektron menjadi pulsa listrik adalah …
1.
a.
Kamar kabut dan detektor
sintilasi
b.
Kamar kabut dan emulsi
film
c.
Detektor sintilasi dan
pencacah Geiger
d.
Pencacah Geiger dan
kamar kabut
e.
Pencacah Geiger dan
emulsi film
Jawaban :
Jawaban : D
Diketahui :
Alat deteksi
radioaktivitas yang mengubah timbunan elektron menjadi pulsa listrik
Ditanyakan :
Pernyataan yang benar
=…?
Jawaban :
Sinar radioaktif berbahaya dan tidak dapat kita lihat sehingga
kita harus memiliki alat untuk mendeteksi (mengenal) adanya sinar radioaktif.
Alat deteksi sinar radioaktif disebut detektor radiasi. Hampir
semua detektor radiasi energi tinggi bekerja berdasarkan prinsip bahwa radiasi
akan memberikan energi pada elektron-elektron dalam bahan yang dilewatinya
sehingga elektron keluar dari atom, dan atom menjadi ion positif (ionisasi).
Diantara detektor radiasi yaitu:
- Pencacah Geiger Muller (GM)
Pencacah Geiger Muller (GM) adalah detektor yang terdiri atas sebuah tabung aluminium yang diisi dengan gas argon bertekanan rendah (10 cmHg) dan seutas kawat yang membentang pada pusat tabung. Dimana kawat bertindak sebagai elektrode positif (anode) dan tabung sebagai elektrode negatif (katode).
Ketika radiasi memasuki tabung GM melalui sebuah jendela tipis
dari mika, gas argon di dalam tabung diionisasi. Ini terjadi karena
partikel-partikel atau foton-foton radioaktif mengetuk elektron-elektron keluar
dari atom-atom gas, membuat atom-atom gas menjadi ion-ion gas bermuatan listrik
positif. Elektron-elektron yang keluar dari atom gas ditarik menuju kawat positif
(anode). Dalam proses pergerakan elektron menuju kawat positif,
elektron-elektron juga akan menumbuk atom-atom gas dan mengionisasinya. Proses
ini menghasilkan timbunan muatan (elektron-elektron) yang akan menghasilkan
pulsa arus pada keluaran tabung karena gas argon yang terionisasi sekarang
dapat melewatkan arus.
- Kamar Kabut
Proses deteksi radiasi pada kamar kabut pertama terjadi ketikas
ebuah sumber radioaktif memancarkan partikel-partikel dalam sebuah kamar udara
yang jauh dengan uap air atau alkohol. Ketika partikel-partikel radioaktif ini
melalui udara, mereka bertumbukan dengan molekul-molekul udara. Tumbukan ini
dapat mengeluarkan elektron-elektron dari molekul-molekul udara, dengan
meninggalkan jejak-jejak ion-ion positif dan negatif. Jika tekanan dalam kamar
dikurangi dengan cara memompa sebagian udara ke luar, udara menjadi lebih
dingin. Keadaan ini memungkinkan partikel-partikel uap superjenuh mengembun
pada ion-ion tersebut, sehingga jejak tetes-tetes uap sepanjang lintasan
ion-ion dapat dilihat.
- Film Fotografis.
Bacquerel telah menggunakan film fotografis ketika ia secara tidak sengaja
menemukan radioaktivitas alami dari uranium. Disini dia menemukan sinar
radioaktif yang telah menghitamkan film. Banyaknya penghitaman pada film akan
menunjukkan sinar radioaktid terdeteksi atau tidak.
27.
Perhatikan reaksi
berikut:
147N+42He+1,2MeV→X+11H
Reaksi inti tersebut
akan lengkap jika inti X adalah …
1.
a.
168O
b.
178O
c.
188O
d.
169P
e.
166N
Jawaban :
Jawaban : B
Diketahui :
147N+42He+1,2MeV→X+11H
Ditanyakan :
Inti X =…?
Jawaban :
Pada setiap reaksi inti akan berlaku kekekalan nomor
massa, kekekalan nomor atom, dan kekekalan energi. Dengan
kata lain: ΣZsebelumreaksi=ΣZsetelahreaksi,ΣAsebelumreaksi=ΣAsetelahreaksi,ΣEsebelumreaksi=ΣEsetelahreaksi.
Maka untuk soal di atas:
147N+42He+1,2MeV→X+11H
Unsur X haruslah
memiliki nomor massa 14+4 = Ax – 1 -> 17
dan nomor atom 7+2 = Zx – 1 -> 8 .
28. Neutron seringkali digunakan untuk menembaki
partikel-partikel dalam beberapa reaksi inti. Hal ini karena neutron …
1.
a.
Bermuatan positif
sehingga ditolak oleh inti atom
b.
Bermuatan negatif
sehingga ditarik oleh inti atom
c.
Tidak bermuatan sehingga
tidak ditolak oleh inti atom
d.
Tidak bermuatan sehingga
tidak ditarik oleh inti atom
e.
Tidak bermuatan dan
massanya dapat diabaikan
Jawaban :
Jawaban : C
Diketahui :
Neutron
Ditanyakan :
Sifat neutron =..?
Jawaban :
Reaksi inti dapat digunakan untuk memproduksi isotop-isotop
radioaktif. Dalam reaksi inti, suatu isotop stabil X (tidak radioaktif)
ditembaki dengan partikel a sehingga menghasilkan isotop baru Y yang
radioaktif. Partikel yang dihasilkan pada reaksi inti ini tidak dibutuhkan
sehingga tidak diamati. Partikel yang sering digunakan untuk menembak inti
sasaran adalah neutron. Hal ini karena neutron tidak bermuatan
ssehingga tidak ditolak oleh inti atom.
29.
Nilai kalor reaksi Q untuk
reaksi 9Be + α -> 12C
+ n adalah …
(9Be = 9,012 sma, α = 4,003 sma, 12C1=12,000 sma; n = 1,009 sma; 1 sma
= 931 MeV)
1.
a.
8,4 MeV
b.
7,3 MeV
c.
6,2 MeV
d.
5,6 MeV
e.
4,9 MeV
Jawaban :
Jawaban : D
Diketahui :
9Be+α→12C+n9Be=9,012smaα=4,003sma12C=12,000sman=1,009sma1sma=9,31MeV
Ditanyakan :
Q =…?
Jawaban :
Hukum kekekalan energi
memberikan :
Q=(∑massakiri−∑massakanan)sma×931MeV/smaQ=[(9,012+4,003)−(12,000+1,009)]×931Q=(13,015−13,009)×931Q=0,006×931Q=5,586MeV
30. Reaksi berantai adalah reaksi …
1.
a.
Penggabungan proton dan
neutron untuk membentuk inti atom
b.
Bergabungnya inti ringan
untuk membentuk inti berat
c.
Pembelahan inti berat
menjadi dua atom lebih ringan
d.
Pembelahan inti berat
terus-menerus yang dipengaruhi oleh neutron-neutron yang dipancarkan oleh
pembelahan inti berat lainnya
e.
Pembakaran uranium dalam
suatu tungku khusus yang disebut reaktor atom
Jawaban :
Jawaban : D
Diketahui :
Reaksi berantai
Ditanyakan :
Pernyataan yang benar =
…?
Jawaban :
Reaksi berantai (chain reactions) adalah sederetan pembelahan inti dimana
neutron-neutron yang dihasilkan dalam tiap pembelahan inti menyebabkan
pembelahan inti-inti lainnya. Jika dalam setiap pembelahan inti, dua neutron
atau lebih hasil pembelahan menyebabkan pembelahan inti-inti lainnya, ini
adalah kondisi reaksi berantai tak terkendali (uncontrolled chain reactions).
31. Suatu proses fisi 23592Umengikuti persamaan 10n+23592U→Ba+Kr+10n . Jika pada reaksi fisi ini dibebaskan energi 200 MeV,
massa neutron = 1,01 sma, massa inti 23592U = 235,04 sma, dan 1 sma =
931 MeV, massa inti (Ba + Kr) adalah
… (dalam sma)
1.
a.
231,08
b.
232,82
c.
233,82
d.
234,04
e.
234,89
Jawaban :
Jawaban : E
Diketahui :
10n+23592U→Ba+Kr+10n
Q = 200 MeV
mn = 1,01 sma
mU = 235,04 sma
Ditanyakan :
m(Ba+Kr) =
… sma
Jawaban :
Hukum kekekalan energi
memberikan:
Q=(∑massakiri−∑massakanan)sma×931MeV/sma200=[(1,01+235,04)−(Ba+Kr+1,01)]×9310,2148=(236,05)−(Ba+Kr+1,01)(Ba+Kr+1,01)=236,05−0,2148(Ba+Kr+1,01)=235,835(Ba+Kr)=235,835−1,01(Ba+Kr)=234,825)
32. Bahan bakar yang digunakan dalam sebuah reaktor
fisi adalah …
1.
a.
Uranium alamiah
b.
Uranium oksida
c.
U-235 murni
d.
U-235 diperkaya
e.
U-238
Jawaban :
Jawaban : D
Diketahui :
Reaktor fisi
Ditanyakan :
Bahan bakar =…?
Jawaban :
Reaktor atom fisi atau reaktor nuklir merupakan tempat terjadinya
reaksi inti berantai terkendali, baik pembelahan inti (fisi) maupun
penggabungan inti (fusi). Umumnya bahan bakar reaktor adalah uranium-235 (U-235).
Isotop ini hanya kira-kira 0,7% terdapat dalam uranium alam sehingga dipelrukan
proses khusus untuk memperkaya (menaikkan persentase) isotop
ini. kebanyak reaktor atom komersial menggunakan uranium dengan jumlah inti
U-235 yang telah diperkaya kira-kira 3%.
33. Berikut ini yang bukan komponen
dasar dari sebuah reaktor atom adalah …
1.
a.
Bahan bakar
b.
Bahan pengendali
c.
Perisai beton
d.
Kondensor
e.
Moderator
Jawaban :
Jawaban : D
Diketahui :
Reaktor atom
Ditanyakan ;
Yang bukan komponen
dasar =…?
Jawaban :
Reaktor atom pertama adalah reaktor termal fisi, yang dibangun
oleh Enrico Fermi pada tahun 1942 di Universitas
Chicago, Amerika Serikat. Hingga kini telah ada berbagai jenis dan ukuran dari
reaktor termal, tetapi semuanya memiliki lima komponen dasar yang sama,
yaitu elemen bahan bakar, moderator neutron, batang pengendali,
pendingin, dan perisai radiasi (radiation shielding).
34. Bagian yang berfungsi untuk memperlambat
kelajuan neutron sehingga neutron-neutron dapat dengan mudah membelah inti atom
adalah …
1.
a.
Batang Pengendali
b.
Kondensor
c.
Moderator
d.
Pendingin
e.
Perisai Beton
Jawaban :
Jawaban : C
Diketahui :
Neutron yang membelah
inti atom
Ditanyakan :
Yang memperlambat =…?
Jawaban :
Neutron-neutron yang mudah membelah inti U-235 adalah
neutron-neutro lambat yang memiliki energi kira-kira 0,04 eV
(atau lebih kecil), sehingga neutron-neutron yang dibebaskan selama proses
pembelahan (fisi) memiliki energi beberapa MeV. Oleh karena itu, sebuah reaktor
atom harus memiliki material yang dapat mengurangi kelajuan neutron-neutron
yang bergerak lebih cepat ini (energinya lebih besar) sehingga neutron-neutron
ini dapat dengan mudah membelah inti. Material yang memperlambat kelajuan
neutron disebut moderator. Material-material moderator dapat berupa
air biasa (H2O), air “berat” (Deuterium oksida, D2O),
ataupun Grafit. Tetapi moderator yang umum digunakan adalah air.
35.
Dalam suatu reaktor
atom, batang-batang pengendali digunakan untuk …
1.
a.
Memperlambat neutron
b.
Mempercepat neutron
c.
Menyerap neutron
d.
Memproduksi neutron
e.
Menembakkan neutron
Jawaban :
Jawaban : C
Diketahui :
Reaktor atom
Ditanyakan :
Fungsi batang pengendali
=…?
Jawaban :
Pada reaktor atom fusi, sebuah mekanisme kendali diperlukan untuk
menjaga reaktor pada keadaan normal atau kondisi kritis. Kendali ini
dilaksanakan oleh sejumlah batang pengendali yang dapat
bergerak keluar masuk teras reaktor. Batang pengendali berupa batang baja yang
mengandung boron atau kadmium sebagai bahan penyerap
neutron. Jika reaktor menjadi superkritis, batang pengendali secara otomatis
bergerak lebih masuk ke dalam teras reaktor untuk menyerap kelebihan neutron
yang menyebabkan kondisi itu sehingga reaktor kembali ke kondisi kritis.
Sebaliknya, jika reaktor menjadi subkritis, batang pengendali sebagian ditarik
menjauhi teras reaktor sehingga lebih sedikit neutron yang diserap. Dengan
demikian, lebih banyak neutron tersedia untuk pembelahan, dan reaktor kembali
ke kondisi kritisnya.
36.
Perhatikan reaksi fusi berikut
:
11H+11H→21d+10e+E
Diketahui massa11H=1,0078 sma ,
massa21d= 2,01410 sma,
massa01e=0,00055 sma,
dan 1 sma = 931 MeV. Nilai E (energi
yang dihasilkan) pada reaksi fusi tersebut adalah …
1.
a.
0,44 MeV
b.
0,88 MeV
c.
0,98 MeV
d.
1,02 MeV
e.
1,47 MeV
Jawaban :
Jawaban : B
Diketahui :
11H+11H→21d+01e+E11H=1,0078sma21d=2,01410sma01e=0,00055sma1sma=931MeV
Ditanyakan :
E =..?
Jawaban :
Hukum kekekalan energi
memberikan :
E=(∑massakiri−∑massakanan)sma×931MeV/smaE=[(1,0078+1,0078)−(2,01410+0,00055)]×931E=[(2,0156)−(2,01465)]×931E=0,00095×931E=0,88MeV
37. Perhatikan reaksi fusi berikut.
21H+31H→42He+10n+Q
Diketahui massa:
21H=2,04741sma;42He=4,003879sma31H=3,016977sma;10n=1,008987sma
Dan 1 sma
= 931 MeV , energi yang dibebaskan pada reaksi fusi
tersebut adalah …
1.
a.
479, 7 MeV
b.
47,97 MeV
c.
4,797 MeV
d.
0,04797 MeV
e.
0,0049 MeV
Jawaban :
Jawaban : B
Diketahui :
21H+31H→42He+10n+Q21H=2,04741sma31H=3,016977sma41He=4,003879sma10n=1,008987sma1sma=931MeV
Ditanyakan :
Q =…?
Jawaban :
Q=(∑massakiri−∑massakanan)sma×931MeV/smaQ=[(2,04741−3,016977)−(4,003879+1,008987)]×931E=[(5,064387)−(5,012866)]×931E=0,051521×931E=47,97MeV
38. Berikut yang bukan merupakan
manfaat radioisotop adalah …
1.
a.
Mendeteksi adanya
penyempitan pembuluh darah
b.
Mendeteksi adanya
kebocoran pipa penyalur minyak
c.
Membunuh sel-sel kanker
d.
Menentukan umur manusia
purba
e.
Memotong lembaran baja
dengan akurat
Jawaban :
Jawaban : E
Diketahui :
Manfaat radioisotop
Ditanyakan :
Yang bukan =…?
Jawaban :
1.
Penggunaan
Radioisotop sebagai Perunut
Radioisotop adalah isotop yang bersifat radioaktif sehingga
jejaknya dapat dikenal misal jejaknya dalam tubuh manusia. Radiosiotop dapat
digunakan sebagai perunut (pencari jejak).
·
- Perunut radioisotop digunakan
dalam pengobatan trombosis (penyakit penyempitan pembuluh darah).
Radioisotop natrium disuntikkan ke dalam tubuh, kemudian aliran natrium
dirunut dengan menggunakan pencacah Geiger. Tempat aliran natrium
terhenti menunjukkan posisi penyempitan pembuluh darah.
- Sebagai pengeruk lumpur pada
pelabuhan dan terowongan. Dengan memasukkan radioisotop silikon ke dalam
lumpur dan kemudian mengukur cara lumpur tersebut terbentuk dan bergerak
dengan detektor radioaktif.
- Kebocoran suatu pipa penyalur minyak
atau gas dapat dirunut dengn menyuntikkan sejumlah radioisotop ke dalam
saluran pipa.
2.
Pemanfaatan
Radioisotop berdasarkan Sifat Radiasinya
Sifat radiasi radioisotop dimanfaatkan dalam dunia pengobatan
untuk membunuh sel kanker yang disebut dengan radioterapi
(radiotherapy)
3.
Penentuan
Umur dengan Radioaktif
Dengan mengukur persentase keaktifan radiasi C-14 dalam tumbuhan,
binatang, atau manusia yang mati, kita dapat menaksir umur kematian mereka.
Teknik seperti inilah yang disebut penentuan umur dengan radioaktif
(radioactive dating).
39. Kegunaan radioisotop I-131 adalah untuk
mendeteksi …
1.
a.
Penyakit paru-paru
b.
Gangguan peredaran darah
c.
Usia fosil
d.
Bibit unggul tanaman
e.
Penyakit getah bening
Jawaban :
Jawaban : E
Diketahui :
Radioisotop I-131
Ditanyakan :
Kegunaan =..?
Jawaban :
Dalam bidang kesehatan, radioisotop dapat digunakan sebagai
perunut (tracer) untuk mendeteksi kerusakan yang terjadi pada suatu
organ tubuh. Selain itu, radiasi dari isotop tertentu juga dapat digunakan
untuk membunuh sel-sel kanker sehingga tidak perlu dilakukan pembedahan untuk
mengangkut jaringan sel kanker tersebut. Diantara kegunaan radioisotop dalam
bidang kesehatan yaitu:
- Iodium-131 (I-131) digunakan
untuk mendeteksi kerusakan pada kelenjar dan untuk mendeteksi jaringan
kanker pada otak.
- Kobalt-60 (Co-60) digunakan
untuk membunuh sel-sel kanker, serta dalam pengobatan leukimia.
- Teknetium-99 (Tc-99) digunakan
untuk membunuh sel-sel kanker.
- Tallium-201 (Tl-201) digunakan
untuk mendeteksi penyakit jantung dan pembuluh darah.
- Besi-59 (Fe-59) digunakan untuk
emmpelajari pembentukan sel darah merah.
- Fosforus-32 (P-32) digunakan
untuk pengobatan penyakit polycythemia rubavera, yaitu
pembentukan sel darah merah yang berlebihan.
40. Sebuah fosil tulang binatang purba ditemukan
dalam tanah. Berdasarkan penelitian laboratorium, sisa karbon C-14 yang
dikandungnya sebesar 12,5% dari karbon C-14 yang dikandung oleh binatang yang
masih hidup. Jika waktu paro waktu C-14 sama dengan 5.600 tahun maka umur fosil
itu adalah …
1.
a.
16.800 tahun
b.
14.000 tahun
c.
11.200 tahun
d.
5.600 tahun
e.
2.800 tahun
Jawaban :
Jawaban : A
Diketahui :
Sisa C-14 = 12,5%
T12=600tahun
Ditanyakan :
t =…?
Jawaban :
N=N0(12)t/T12
Jika sisa C-14 adalah
12,5%, ini berarti:
N=12,5% N0=18N0
Maka :
N=N0(12)t/T12
18N0=N0(12)t/T1218=(12)tT12(12)3=(12)t5.600t=3×5600t=16.800tahun
II. ESAI
Kerjakan soal-soal berikut di buku latihan Anda. Jika diperlukan
gunakan g = 10 m/s2, c = 3 x 108 m/s, e = 1,6 x 10-19 C,
me = 9,1 x 10-31 kg, h = 6,6 x 10-34 Js,
1 u = 1,6 x 10-27 kg, 1 u = 1 sma = 931 MeV, 10n=1,0086 u, 11H = 1,0078 u, NA = 6,02 x 1023 mol,
dan 1 tahun = 365 hari
A.
Perkembangan Teori Atom
1.
Sebuah proton (partikel
bermuatan positif) melewati daerah medan magnetik 1,2 T tanpa
mengalami pembelokan karena diseimbangkan oleh medan listrik 8,4 x 103 N/C.
Berapa kelajuan gerak proton?
Diketahui :
E = 8,4 x 103 N/C
B = 1,2 T
Ditanyakan :
v =…?
Jawaban :
Fmagnet=FlistrikBqv=qEv=EBv=8,4×1031,2v=7000m/s
Kesimpulan.
Jadi, kelajuan gerak
proton adalah 7000 m/s.
2.
Dalam sebuah tabung
sinar katode, elektron keluar dari katode menuju anode dengan kelajuan 4 x 107 m/s.
Berapakah beda potensial antara anode dan katode ?
Diketahui :
v = 4 x 107 m/s
Ditanyakan :
ΔV =…?
Jawaban :
Misal beda potensial katode dan anode adalah ΔV, maka elektron
akan memiliki energi potensial sebesar qeΔV. Dengan energi sebesar
qΔV elektron bergerak menuju anode sehingga kecepatannya bisa dihitung
sebagai berikut:
qeΔV=12mev2ΔV=mev22qe
Dengan nilai qe =
1,6 x 10-19 C dan me =
9,1 x 10-31 kg maka:
ΔV=mev22qeΔV=(9,1×10−31)×(4×107)22×(1,6×10−19)ΔV=1,456×10−153,2×10−19ΔV=4550volt
Kesimpulan.
Jadi, beda potensial
antara anode dan katode adalah 4550 volt.
3.
Sebuah partikel
bermuatan bergerak melalui sutau pemilih kecepatan dengan kelajuan konstan pada
suatu garis lurus. Medan listrik dari pemilih kecepatan adalah 1,4 x 103 N/C,
sedangkan medan magnetiknya adalah 0,114 T. Ketika medan listrik
ditiadakan, partikel bermuatan itu bergerak pada suatu lintasan melingkar
dengan jari-jari 5,80 cm. Tentukan nilai perbandingan antara muatan
dan massa partikel itu.
Diketahui :
E = 1,4 x 103 N/C
B = 0,114 T
r = 5,80 cm = 0,058 m
Ditanyakan :
qm =…?
Jawaban :
1.
Tentukan kecepatan v,
Fmagnet=FlistrikBqv=qEv=EBv=1,4×1030,114v=12,28×103m/s
2.
Mencari perbandingan
antara muatan dan massa partikel
Fmagnet=FsentripetalBqv=mv2rqm=v2rBv=vBrqm=12,28×1030,114×0,058qm=1,85×106C/Kg
Kesimpulan.
Jadi, nilai perbandingan
antara muatan dan massa partikel itu adalah 1,85 x 106 C/Kg.
4.
Sebuah tetesan minyak
bermassa 8 x 10-15 kg dan mengandung lima buah
elektron, memasuki ruang di antara pasangan keping sejajar melalui lubang pada
keping A (lihat gambar). Dengan mengatur besar tegangan antara
kedua keping, tetesan minyak tersebut dibuat diam di dalam ruang di antara
kedua keping. Jarak antara kedua keping d = 2 cm.
1.
a.
Keping manakah yang
bermuatan negatif ?
b.
Hitung besar tegangan
antara keping A dan B
Diketahui :
m = 8 x 10-15 kg
n = 5
d = 2 cm = 0,02 m
Ditanyakan :
a.
Keping yang negatif
b.
V
Jawaban :
a.
Percobaan tetes minyak
adalah percobaan Millikan yang mana dua keping logam sejajar horizontal
dipisahkan
dnegan jarak d dalam orde milimeter. Minyak
disemprotkan dari bagian atas keping oleh alat penyemprot tetesan. Beberapa
tetesan minyak memasuki lubang kecil pada keping A. tetesan minyak
bermuatan listrik karena gesekan.
Sebuah tetesan minyak yang masuk melalui lubang pada keping A diamati
dengan teleskop. Tetesan minyak terlihat di teleskop menyerupai bintang-bintang
kecil yang sangat terang. Jika keping A dan B tidak
diberi muatan listrik, tetesan minyak akan bergerak lurus ke bawah karena
keseimbangan antara tiga gaya yang bekerja pada tetesan minyak: gaya berat,
gaya apung udara, dan gaya gesekan udara. Jika keping A diberi
muatan listrik positif (+) dan keping B diberi muatan listrik
negatif (-), dengan mengatur besar kuat medan listrik E di
antara kedua keping, tetesan minyak dapat dibuat diam di antara kedua keping.
Pada saat ini, gaya listrik yang dihasilkan medan listrik, qEm
seimbang dengan berat tetesan minyak, mg.
Berdasarkan percobaan millikan tersebut, maka di
dalam soal karena tetesan minyak tersebut dibuat diam di dalam ruang di antara
kedua keping maka berarti keping A diberi muatan listrik positif (+) dan keping
B diberi muatan listrik negatif (-).
b.
Besar tegangan antara
keping A dan B
Pada saat tetesan minyak dibuat diam di dalam ruang diantara kedua
keping maka saat itu gaya listrik yang dihasilkan medan listrik, qEm
seimbang dengan berat tetesan minya, mg.
qE=mg
Anggap tetesan minyak mengandung n elektron dengan
muatan tiap elektron adalah e, maka persamaannya menjadi seperti
berikut:
neE=mg
E=mgne…..(1)
Dimana E juga
dapat dicari dengan membagi tegangan dengan jarak:
E=VABd…..(2)
Maka dengan
mensubstitusikan persamaan (1) dan (2) didapatkan:
VABd=mgneVAB=mgdne
Bila muatan sebuah
elektron adalah e = 1,6 x 10-19 maka:
VAB=(8×10−15)×10×0,025×(1,6×10−19)VAB=2000VVAB=2kV
Kesimpulan.
Jadi, keping yang
bermuatan negatif adalah keping B dan besar tegangan antara
keping A dan B adalah 2 kV.
5.
Suatu tetes minyak
dengan massa 2 x 10-15 kg ditahan diam di udara
ketika suatu medan listrik diberikan di antara dua keping sejajar. Jika tetes
minyak membawa 3 elektron, hitung besar medan listrik itu.
Diketahui :
m = 2 x 10-15 kg
n = 3 elektron
Ditanyakan :
E = …?
Jawaban :
Pada keadaan setimbang, pada elektron bekerja 2 gaya yaitu W gaya
berat yang mengarah ke bawah (pusat bumi) dan F gaya listrik yang mengarah ke
atas (dari medan listrik) dan berlaku:
∑F = 0
F = W
q E = m g
Dengan nilai g =
10 m/s2
q E = (2 x 10-15) x 10
= 20 x 10-15 N
Bila muatan sebuah
elektron adalah e = 1,6 x 10-19 maka:
q = n x e
q = 3 x 1,6 x 10-19
q = 4,8 x 10-19 C
Maka:
q E = 2 x 10-15 N
E=20×10−154,8×10−19E=41,67×103N/C
Kesimpulan.
Jadi, besar medan
listrik itu adalah 41,67 x 103 N/C.
6.
Berapakah panjang
gelombang terpendek dan terpanjang pada :
1.
a.
Deret Brackett,
b.
Deret Pfund
Catatan = 1∞=0
Diketahui :
Panjang gelombang
Ditanyakan :
a.
Deret Brackett,
b.
Deret Pfund
Jawab:
a.
Deret BrackettUntuk
deret brackett nilai n = 4, maka dengan menggunakan rumus:
1λ=R(1n2−1m2)denganm=(n+1)(n+2),..danR=1,097×107m−1
Berdasarkan rumus tersebut, panjang gelombang berbanding terbalik
dengan nilai m. Dalam hal ini berarti, panjang gelombang terpendek
adalah saat m paling besar dan panjang gelombang terpanjang
adalah saat m paling kecil.
Gelombang terpanjang adalah :
1λ=R(1n2−1m2)(1,097×107)×(142−152)λ=405,15nm
Gelombang
terpendek adalah :
1λ=R(1n2−1m2)(1,097×107)×(142−1∞2)λ=1,45μm
b.
Deret Pfund
Untuk deret pfund
nilai n = 5, maka dengan menggunakan rumus :
1λ=R(1n2−1m2)denganm=(n+1)(n+2),..danR=1,097×107m−1
Berdasarkan rumus tersebut, panjang gelombang berbanding terbalik
dengan nilai m. Dalam hal ini berarti, panjang gelombang terpendek
adalah saat m paling besar dan panjang gelombang terpanjang
adalah saat m paling kecil.
Gelombang terpanjang adalah :
1λ=R(1n2−1m2)(1,097×107)×(152−162)λ=7,45μm
Gelombang terpendek
adalah :
1λ=R(1n2−1m2)(1,097×107)×(152−1∞2)λ=2,27μm
7.
Panjang gelombang
terpendek dari suatu deret adalah 1,45μ. Deret apakah ini ?
Diketahui :
λterpendek =
1,45μm = 1,45 x 10-6 m
Ditanyakan :
Jenis deret =…?
Jawaban :
Sebelum mengerjakan soal tersebut, kita harus mengetahui
jenis-jenis deret, yaitu: deret Lyman (n = 1); Balmer (n =
2); Paschen (n = 3); Brackett (n = 4); dan Pfund (n =
5).
Berdasarkan rumus berikut:
1λ=R(1n2−1m2)denganm=(n+1)(n+2),..danR=1,097×107m−1
Karena ini merupakan
panjang gelombang terpendek maka m = ∞, lalu besar n dapat
ditentukan dengan (1∞=0):
11,45×10−6=(1,097×107)×(1n2−1∞2)
n2=(1,097×107)×(1,45×10−6)
n=16−−√=4→DeretBrackett
Kesimpulan.
Jadi, deret ini adalah
deret Brackett.
8.
Untuk atom hidrogen pada
orbit Bohr n = 2, tentukan :
1.
a.
Jari-jari orbit,
b.
Gaya listrik yang
bekerja pada elektron,
c.
Gaya sentripetal pada
elektron,
d.
Kelajuan elektron.
Bandingkan dengan kelajuan cahaya.
Diketahui :
Orbit Bohr, n =
2
Ditanyakan :
a.
r
b.
Flistrik
c.
Fsentripetal
d.
v
Jawaban :
a.
Jari-jari orbitSecara
umum rumus jari-jari stasioner dinyatakan dalam a0 sebagai
berikut:
rn=n2a0
Dengan
nilai a0=0,528A˚=0,528×10−10m, maka:
r2=22(0,528×10−10)r2=2,112A˚r2=2,112×10−10m
b.
Gaya listrikGaya listrik
(coulomb) ditentukan berdasarkan:
Flistrik=ke2r2
Dengan
nilai k=9×109Nm2/C2dan e=1,6×10−19Cmaka:
Flistrik=(9×109)×(1,6×10−19)2(2,112×10−10)2Flistrik=5,165×10−9N
c.
Gaya sentripetalGaya
sentripetal adalah sama dengan gaya listrik (coulomb).
Flistrik = Fsentripetal = 5,165 x
10-9 N
d.
Kelajuan elektron
Berdasarkan gaya
sentripetal dapat ditentukan kelajuan elektron sebagai berikut:
Fsentripetal=mv2r2v=Fsentripetal×r2m−−−−−−−−−−−−√
Dengan nilai m =
9,1x10−31kg maka:
v=(5,165×10−9)×(2,112×10−10)2(9,1×10−31)−−−−−−−−−−−−−−−−−−√v=15,91m/s
Maka perbandingan vc=15,913×108=5,3×10−8
Kesimpulan.
Jadi, jari-jari orbit adalah 2,112 x 10-10 m;
gaya listrik yang bekerja pada elektron sama dengan gaya sentripetal pada
elektron yaitu Flistrik = Fsentripetal =
5,165 x 10-9 N; dan kelajuan elektron adalah
15,91 m/s serta perbandingan dengan kelajuan cahaya adalah 5,3
x 10-8.
9.
Jika jari-jari pada orbit
ke-2 untuk atom hidrogen adalah 2.112Å, tentukan jari-jari pada orbit ke-3,
ke-4, dan ke-5.
Diketahui :
r2=2,112A˚
Ditanyakan :
r3,r4,danr5
Jawaban :
Secara umum rumus
jari-jari stasioner dinyatakan dalam a0 sebagai
berikut:
rn=n2a0
Dengan nilai a0=0,528A˚=0,528×10−10m, maka:
r3=32(0,528×10−10)r3=4,752A˚r3=4,752×10−10m
r4=42(0,528×10−10)r4=8,448A˚r4=8,448×10−10m
r5=52(0,528×10−10)r5=13,2A˚r5=13,2×10−10m
Kesimpulan.
Jadi, jari-jari pada orbit ke-3 adalah 4,752Å, sedangkan jari-jari
pada orbit ke-4 adalah 8,448Å, dan jari-jari pada orbit ke-5 adalah 13,2Å.
10. Sebuah elektron bertumbukan dengan sebuah atom
gas hidrogen yang berada dalam kulit ke dua. Berapakah energi minimum
(dalam eV) yang harus elektron berikan untuk menyebabkan hidrogen
memancarkan sebuah foton garis Balmer?
Diketahui :
n = 2
Ditanyakan :
Energi minimum =…?
Jawaban :
En=−13,6n2eVdengann=1,2,3,…
Berdasarkan rumus
tersebut maka:
En=−13,622En=−3,4eV
Kesimpulan.
Jadi, energi minimum
yang harus elektron berikan untuk menyebabkan hidrogen memancarkan sebuah foton
garis Balmer adalah -3,4 eV
11. Energi ionisasi atom hidrogen adalah 3,4 eV.
Hitung :
1.
a.
Kelajuan sebuah elektron
yang tepat dapat mengionisasi atom hidrogen.
b.
Panjang gelombang
minimum yang dapat dipancarkan atom hidrogen.
Diketahui :
E = 3,4eV
Ditanyakan :
a.
v
b.
λ
Jawaban :
a.
Kelajuan Elektron, v
Ek=Eionisasi
12mv2=13,6eVv=13,6×2m−−−−−√
Dengan
nilai me = 9,1 x 10-31 kg dan
1 eV = 1,6 x 10-19 J maka:
v=13,6×2×(1,6×10−19)9,1×10−31−−−−−−−−−−−−−√v=2,19×106m/s
b.
Panjang gelombang
minimum
Panjang gelombang
minimum terjadi jika transisi elektron dari n = 1 ke n =
∞. Jadi:
ΔE=−13,6(1∞2−112)
hf=13,6eV
hcλ=13,6×(1,6×10−19)λ=hc13,6×(1,6×10−19)
Dengan nilai h =
6,6 x 10-34 J s dan c = 3 x 108 m/s maka:
λ=(6,6×10−34)x(3×108)13,6×(1,6×10−19)λ=9,14×10−7mλ=914nm
Kesimpulan.
Jadi, kelajuan sebuah elektron yang tepat dapat mengionisasi atom
hidrogen adalah 2,19 x 106 m/s dan panjang
gelombang minimum yang dapat dipancarkan atom hidrogen adalah 914nm.
12. Sebuah atom hidrogen dalam keadaan n =
3 membuat transisi ke keadaan dasar dengan memancarkan sebuah foton. Hitung
panjang gelombang foton yang dipancarkan.
Diketahui :
m = 3
n =1
Ditanyakan :
λ =…?
Jawaban :
Dengan menggunakan rumus
Balmer maka transisi elektorn menyebabkan panjang gelombang foton:
1λ=R(1n2−1m2)
Dengan nilai R =
1,097 x 107 maka:
1λ=1,097×107(112−132)λ=1,025×10−7mλ=102,5nm
Kesimpulan.
Jadi, panjang gelombang
foton yang dipancarkan adalah 102,5 nm.
B.
Inti Atom dan Radioaktivitas
13.
Tentukan banyaknya
proton, neutron, dan elektron dalam isotop-isotop berikut :
1.
a.
168O
b.
8438Sr
c.
14054Xe
d.
23592U
Diketahui :
Isotop
Ditanyakan :
Proton, neutron, dan
elektron =…?
Jawaban :
Jumlah proton dalam suatu inti atom disebut nomor atom,
dilambangkan oleh Z. Adapun jumlah nukleon (proton dan neutron)
dalam inti atom disebut nomor massa, dilambangkan oleh A. Jika
unsur dilambangkan oleh X, inti atom dengan nomor atom dan nomor massa tertentu
disebut nuklida. Sebuah nuklida dilambangkan sebagai berikut:
AZX
Dengan begitu dapat
ditentukan jumlah proton, elektron dan neutron sebagai berikut:
Jumlah proton = Z
Jumlah neutron = A -Z
Jumlah elektron = Z
(untuk atom netral)
a.
168O
Z
= 8 = proton = elektron
A
= 16 –>neutron = A -Z = 16 – 8 = 8
Maka
proton = 8, neutron = 8, dan elektron = 8
b.
8438Sr
Z
= 38 = proton = elektron
A
= 84 –>neutron = A -Z = 84 – 38 = 46
Maka
proton = 38, neutron = 46, dan elektron = 38
c.
14054Xe
Z
= 54 = proton = elektron
A
= 140 –>neutron = A -Z = 140 – 54 = 86
Maka
proton = 54, neutron = 86, dan elektron = 54
d.
23592U
Z = 92 = proton =
elektron
A = 235 –>neutron = A
-Z = 235 – 92 = 143
Maka proton = 92,
neutron = 143, dan elektron = 92
14. Proton-proton dan ion-ion bermuatan tunggal
dilewatkan secara bergantian melalui selektor kecepatan yang sama ke dalam
kamar pembelokan dari sebuah spektrometer massa. Proton-proton menempuh
lintasan setengah lingkaran dengan jari-jari 10 mm. Berapakah perbedaan
antara jari-jari setengah lingkaran yang ditempuh oleh ion-ion bermuaan
tunggal?
Diketahui :
Proton-proton dan
ion-ion bermuatan tunggal dilewatkan secara bergantian melalui selektor
kecepatan yang sama ke dalam kamar pembelokan dari sebuah spektrometer massa
Ditanyakan :
Jari-jari setengah
lingkaran =…?
Jawaban :
Muatan mengamali lintasan 12lingkaran karena bergerak dalam medan magnet
dan mendapatkan gaya Lorentz di dalam spektrometer massal. Gaya Lorentz ini
menyebabkan lintasan yang tadinya lurus menjadi 12 lingkaran. Gaya Lorentz arahnya selalu ke
pusat jadi merupakan gaya sentripetal.
qvB=mv2RR=mvqB
Jika ion bermuatan tunggal dan proton mempunyai kecepatan yang
sama dan tetunya di dalam spektrometer mendapatkan induksi magnetik yang sama,
maka jari-jari lintasan proton dan ion dapat diperbandingkan sebagai berikut:
RPROTONRION=mPROTONqPROTONmionqion
Ion bermuatan tunggal adalah satu atom yang terdiri dari satu
muatan, maka kemungkinan ion ini adalah ion negatif yang terdiri dari 1
elektron, atau ion positif yang terdiri dari 1 proton.
- Untuk Ion Positif = 1 proton
Karena sama-sama proton
maka jari jari setengah lingkaran ion adalah:
RPROTONRION=mPROTONqPROTONmionqionRPROTONRION=mPROTONqPROTONmPROTONqPROTONRPROTONRION=10mm
- Untuk Ion Negatif = 1 elektron
RPROTONRION=mPROTONqPROTONmELEKTRONqELEKTRON
RION=RPROTONxmELEKTRONqELEKTRONmPROTONqPROTONRION=RPROTONxmELEKTRONxqPROTONqELEKTRONxmPROTON
RION=10×(9,11×10−31)×(1,6×10−19)(1,6×10−19)×(1,67×10−27)RION=5,45×10−3mm
Perbedaan antara
jari-jari setengah lingkaran yang ditempuh oleh ion-ion bermuatan tunggal dan
proton bila:
RPROTONRION=105,45×10−3RPROTONRION=1.834
15.
Jika massa atom triton
adalah 3,016 sma, tentukan defek massa, energi ikat, dan energi
ikat per nukleon dari triton.
Diketahui :
Massa atom triton =
3,016 sma
Massa triton –> Nomor
massa = 3, nomro atom = 1
Ditanyakan :
Δm, ΔE, dan ΔEA=…?
Jawaban :
- Menentukan defek massa
Jika nomor massa = 3 dan nomor atom = 1 maka proton = 1, elektron
= 1 , dan neutron = 2.
Massa proton = 1,007276; massa elektron = 0,000549; dan massa
neutron = 1,008665.
∑m=(p.mp)+(e.me)+(n.mn)∑m=(1×1,007276)+(1×0,000549)+(2×1,008665)∑m=1,007276+0,000549+2,01733∑m=3,025155
Defek massa Δm adalah selisih massa antara gabungan
massa nukleon-nukleon pembentuk inti dengan massa inti stabilnya, secara
matematis ditulis:
Δm=(∑m)−mstabil
Maka:
Δm=3,025155−3,016Δm=9,155×10−3sma
- Menentukan energi ikat
Energi ikat inti adalah energi yang diperlukan untuk memutuskan
inti menjadi proton-proton dan neutron-neutron pembentuknya. Secara matematis
dapat dicari dengan:
ΔE=Δmc2
Dengan nilai c =
3 x 108 m/s maka:
ΔE=(9,155×10−3)×(3×108)2ΔE=8,24×1014J
- Menentukan energi ikat per nukleon
Untuk memisahkan nukleon-nukleon dalam inti perlu diberikan energi
minimal sebesar energi ikatnya. Jika energi ikat total dibagi dengan banyaknya
nukleon yang dikandung sebuah atom, kita peroleh energi ikat per nukleon adalah
ΔEA, maka:
ΔEA=8,24×10143ΔEA=2,74×1014J
Kesimpulan.
Jadi, defek massa atom
triton adalah 9,55 x 10-3 sma; sedangkan energi ikatnya
adalah 8,24 x 1014 J; dan energi ikat per nukleonnya
adalah 2,74 x 1014 J.
16. Tentukan energi ikat dan energi ikat per nukleon
untuk :
1.
a.
5626Fe(55,9349sma);
b.
23892U(238,0507sma);
c.
4020Ca(39,962591sma).
d.
Dari ketiga
nuklida tersebut, manakah yang paling stabil? Jelaskan.
Diketahui :
Nuklida
Ditanyakan :
Energi ikat dan energi
ikat per nukleon =…?
Jawaban :
Catatan awal perlu diketahui bahwa massa proton = 1,007276; massa
elektron = 0,000549; dan massa neutron = 1,008665
a.
5626Fe(55,9349sma)
5626FeA=56;Z=26proton=26,elektron=26,danneutron=56−26=30
∑m=(p.mp)+(e.me)+(n.mn)∑m=(26×1,007276)+(26×0,000549)+(30×1,008665)∑m=26,189176+0,014274+30,25995∑m=56,4634Δm=56,4634−55,9349Δm=0,5285
o Energi Ikat
ΔE = Δm c2
Dengan
nilai c = 3 x 108 m/s maka:
ΔE = 0,5285 x (3 x 108)2 =
4,75 x 1016 J
o Energi Ikat per Nukleon
ΔEA=4,75×101656ΔEA=8,49×1014J
b.
23892U(238,0507sma)
23892UA=238;Z=92proton=92,elektron=92,danneutron=146
∑m=(p.mp)+(e.me)+(n.mn)∑m=(92×1,007276)+(92×0,000549)+(146×1,008665)∑m=92,669392+0,050508+147,26509∑m=239,98499Δm=239,98499−238,0507Δm=1,93429
o Energi Ikat
ΔE = Δm c2
Dengan
nilai c = 3 x 108 m/s maka :
ΔE = 1,93 429 x (3 x
108)2 = 1,74 x 1017 J
o Energi Ikat per Nukleon
ΔEA=1,74×1017238ΔEA=7,31×1014J
c.
4020Ca(39,962591sma)
4020CaA=40;Z=20proton=20,elektron=20,danneutron=20
∑m=(p.mp)+(e.me)+(n.mn)∑m=(20×1,007276)+(20×0,000549)+(20×1,008665)∑m=20,14552+0,01098+20,1733∑m=40,3298Δm=40,3298−39,962591Δm=0,367209
o Energi Ikat
ΔE = Δm c2
Dengan
nilai c = 3 x 108 m/s maka :
ΔE = 0,367209 x (3 x
108)2 = 3,3 x 1016 J
o Energi Ikat per Nukleon
ΔEA=3,3×101640ΔEA=8,26×1014J
d.
Nuklida yang
paling stabil
Semakin stabil sebuah inti, semakin besar energi yang diperlukan
untuk memutuskan inti tersebut (energi ikat). Maka dari ketiga nuklida di atas,
nuklida yang paling stabil adalah nuklida dengan energi ikat yang paling besar
yaitu 1,74 x 1017 J untuk nuklida 23892U.
17. Massa isotop 147N. Hitung defek massa, energi ikat, dan energi ikat per nukleon
isotop tersebut. (Massa proton = 1,008 sma, massa neutron =
1,009 sma, massa elektron = 0,0005, dan 1 sma =
931 MeV)
Diketahui :
147N=14,0075 sma
Ditanyakan :
Δm, ΔE, dan ΔEA =…?
Jawaban :
(Massa proton = 1,008
sma, massa neutron = 1,009 sma, massa elektron = 0,0005, dan 1 sma = 931 MeV)
147NA=14;Z=7proton=7,elektron=7,danneutron=7
- Defek massa
∑m=(p.mp)+(e.me)+(n.mn)∑m=(7×1,007276)+(7×0,000549)+(7×1,008665)∑m=7,056+0,0035+7,063∑m=12,1225smaΔm=14,1225−14,0075Δm=0,115smaΔm=0,115u
- Energi Ikat
ΔE=Δmx(931MeV/u)ΔE=0,115u×(931MeV/u)ΔE=107,065MeV
- Energi Ikat per Nukleon
ΔEA=107,06514ΔEA=7,6475MeV
Kesimpulan.
Jadi, defek massa 147N adalah 0,115 u; sedangkan energi ikatnya adalah
107,065 MeV; dan energi ikat per nukleonnya adalah 7,6475 MeV.
18. Dua nuklida yang memiliki nomor massa sama
disebut sebagai isobar. Hitung perbedaan energi ikat per nukleon untuk isobar2311Na dan 2312Mg . Bagaimana cara Anda menghitung perbedaan
ini? (Massa 2311Na=22,9897sma;2312Mg=22,9941sma )
Diketahui :
2311Nadan2312Mg
2311Na=22,9897sma2312Mg=22,9941sma
Ditanyakan :
Perbedaan energi ikat
keduanya =…?
Jawaban :
1.
2311Na
2311Na→A=23;Z=11→proton=11,elektron=11,danneutron=12
- Defek massa
∑m=(p.mp)+(e.me)+(n.mn)∑m=(11×1,008)+(11×0,0005)+(12×1,008)∑m=11,088+0,0055+12,108∑m=23,2025smaΔm=23,2015−22,9897Δm=0,2118smaΔm=0,2218u
- Energi Ikat
ΔE=Δm×(931MeV/u)ΔE=0,2218u×(931MeV/u)ΔE=197,1858MeV
- Energi ikat per nukleon
ΔEA=197,185823ΔEA=8,57MeV
2.
23Mg
2312MgA=23;Z=12proton=12,elektron=11,danneutron=11
- Defek massa
∑m=(p.mp)+(e.me)+(n.mn)∑m=(12×1,008)+(12×0,0005)+(11×1,009)∑m=12,096+0,006+11,099∑m=23,201smaΔm=23,201−22,9941Δm=0,2069smaΔm=0,2069u
- Energi Ikat
ΔE=Δm×(931MeV/u)ΔE=0,2069u×(931MeV/u)ΔE=192,6239MeV
- Energi ikat per nukleon
ΔEA=192,623923ΔEA=8,37MeV
Maka
perbedaan energi ikat
kedua nuklida di atas adalah:
8,57−8,37=0,2MeV
Kesimpulan.
Jadi, perbedaan energi ikat per nukleon untuk isobar 2311Nadan 2312Mg adalah 0,2 MeV.
1.
Energi ikat dari 4020Caadalah 361,7 MeV. Tentukan massa
atom Ca-42 (dalam sma).
Diketahui :
4220Ca→ΔE=361,7MeV
Ditanyakan :
Massa atom Ca-42
(dalam sma) =…?
Jawaban :
1.
Menentukan defek massa
ΔE=Δm×(931MeV/u)Δm=ΔE931MeV/uΔm=361,7MeV931MeV/uΔm=0,3885
2.
Menentukan massa
gabungan
4220CaA=42;Z=20proton=20;elektron=20;neutron=22
∑m=(p.mp)+(e.me)+(n.mn)∑m=(20×1,008)+(20×0,0005)+(22×1,009)∑m=20,16+0,01+22,198∑m=42,368sma
3.
Menentukan massa atom
Ca-42
Δm = massa
gabungan = massa atom
massa atom = massa
gabungan – Δm = 42,368 – 0,3885 = 41,9795 sma
Kesimpulan.
Jadi, massa atom Ca-42
adalah 41,9795 sma.
20. Berapakah energi kinetik partikel alfa yang
dipancarkan dalam peluruhan inti? Anggaplah inti meluruh dalam keadaan diam dan
seluruh energi reaksi diberikan ke energi kinetik partikel alfa. (U-232 =
232,0371, Th-228 = 228,0287).
Diketahui :
U-232 = 232,0371
Th-228 = 228,0287
Ditanyakan :
Energi Kinetik =…?
Jawaban :
Berdasarkan soal di atas
maka persamaan reaksinya dapat ditulis:
23293U→42α+22892Th
Sesuai hukum kekekalan
energi:
Qreaktan=(mreaktan−mproduk)×931MeV/uQreaktan=(mU−mTh−mα)×931MeV/u
Dengan nilai mα=
4,0026 maka:
Q = (232,0371 – 228,0287 – 4,0026) x 931 =
5,3998 MeV
Energi kinetik dari
partikel alfa adalah:
Ek=(A−4)QAEk=(232−4)×5,3998232Ek=5,3067MeV
Kesimpulan.
Jadi, energi kinetik
partikel alfa adalah 5,3998 MeV.
21. Berapakah energi maksimum elektron yang
dipancarkan dalam peluruhan beta dari ?31H
(H-3 = 3,01605 sma, He-3 = 3,01603 sma)
Diketahui :
H – 3 = 3,01605 sma
He-3 = 3,01603 sma
Ditanyakan :
Ek =…?
Jawaban :
Berdasarkan soal di atas
maka dapat diketahui persamaan reaksinya adalah:
31H→3H+β+Q
Dari persamaan tersebut
maka:
Q = (mreaktan – mproduk)
x 931 MeV/u
Q = (3,01605 – 3,01603) x 931
Q = 0,01862 MeV
Q = 18,62 keV
Energi maksimum elektron
dalam peluruhan beta sama dengan:
Ek = Q =
18,62 keV
Kesimpulan.
Jadi, energi maksimum
elektron yang dipancarkan dalam peluruhan beta dari 31H adalah 18,62 keV.
22. Sebuah inti 23293Umemancarkan partikel dengan energi kinetik 5,32 MeV.
Apakah inti hasil peluruhannya dan berapakah massa atomnya (dalam sma) secara
pendekatan ?
(U-232 = 232,0371 sma, α = 4,0026 sma)
Diketahui :
E = 5,32 MeV
U-232 = 232,0371 sma
α = 4,0026 sma
Ditanyakan :
Inti hasil peluruhan dan
massa atomnya =…?
Jawaban :
Berdasarkan soal di atas
maka persamaan reaksinya dapat ditulis:
23293U→42α+X+E
Dan berdasarkan hukum
kekekalan energi :
(Ek=(A−4)QAQ=Ek×AA−4Q=(5,32)(232)232−4Q=5,4133MeV
Sedangkan:
Q = (mreaktan – mproduk)
x 931 MeV/u
5,4133 = (232,0371 –
4,0026 – X) x 931 MeV/u
5,4133931 = 228,0345 – X
5,81 x 10-3 =
228,0345 – X
X = 228,0345 – (5,71 x
10-3)
X = 228,02869 sma
Dari massa atomnya maka
inti hasil peluruhannya adalah Th-228.
Kesimpulan.
Jadi, inti hasil
peluruhannya adalah Th-228 dengan massa atomnya 228,02869 sma.
23. Energi kinetik maksimum partikel β yang
dipancarkan dalam peluruhan tritium (31H) adalah 19 keV. Jika massa tritrium adalah
3,0160 sma, berapakah massa inti hasil peluruhannya?
Diketahui :
Ek = 19 keV =
19 x 10-3 MeV
H-3 = 3,0160 sma
Ditanyakan :
Massa inti hasil
peluruhan =…?
Jawaban :
Jika massa β=11.840=5,43x10−4sma dan energi maksimum elektron dalam peluruhan
beta sama dengan Q maka :
Q = (mreaktan – mproduk)
x 931 MeV/u
19 x 10-3 =
(3,0160 – mproduk) x 931 MeV/u
19x10−3931= 3,0160 – mproduk
2,04 x 10-5 =
3,0160 – mproduk
mproduk =
3,0160 – 2,04 x 10-5
mproduk =
3,0159 sma
Kesimpulan.
Jadi, massa inti hasil
peluruhannya adalah 3,0159 sma.
24. Sinar γ menguraikan sebuah inti deuterium
menjadi sebuah proton dan sebuah neutron. Massa sebuah inti deuterium adalah
2,015 sma, sebuah proton adalah 1,008 sma dan
sebuah neutron adalah 1,009 sma . Tentukan panjang gelombang
maksimum dari sinar yang datang.
Diketahui :
21H=2,015 sma
mp = 1,008 sma
mn = 1,009 sma
Ditanyakan :
λmin =…?
Jawaban :
ΔE = Δm x
931 MeV/u
ΔE = (mH – mp – mn)
x 931 MeV/u
ΔE = (2,015
– 1,008 – 1,009) x 931 MeV/u
ΔE = -0,002
x 931 MeV/u
ΔE = -1,862 MeV
Kemudian substitusikan
ke dalam persamaan:
E=hcλλ=hcE
Dengan nilai h =
6,6 x 10-34 Js, c = 3 x 108 m/s dan e =
1,6 x 10-19 C maka:
λ=(6,6×10−34)×(3×108)1,862×(1,6×10−19)λ=6,68×10−7mλ=668nm
Kesimpulan.
Jadi, panjang gelombang
maksimum dari sinar γ yang datang adalah 668 nm.
C. Peluruhan
25. Waktu paro suatu bahan radioaktif adalah 10 jam.
Radiasi awal cuplikan diukura dan didapat aktivitas 1.200 hitungan per menit.
Berapakah aktivitasnya setelah :
1.
a.
10 jam;
b.
20 jam;
c.
30 jam;
d.
40 jam?
Diketahui :
T12= 10 jam = 36000 s
t = 10 jam, 20 jam, 30 jam, 40 jam
A0 = 1.200cacahmenit= 72.000 cacah/s = 72.000 Bq
Ditanyakan :
A =…?
Jawaban :
T12=ln2λ=0,693λα=0,693T1α=0,69336000α=1,925×10−5s−1
a.
t = 10 jam = 36000
A = A0 e-λt
A = 72000
(2,718) -(1,925 x 10-5) (36000)
A = 51762,50881
cacah/s
A = 862,7 cacah/menit
b.
t = 20 jam = 72000
A = A0 e-λt
A = 72000 (2,718) -(1,925
x 10-5) (72000)
A = 18005,29928
cacah/s
A = 300,08
cacah/menit
c.
t = 30 jam = 108000
A = A0 e-λt
A = 72000
(2,718) -(1,925 x 10-5) (108000)
A = 9003,974 cacah/s
A = 150,06
cacah/menit
d.
t = 40 jam = 144000
A = A0 e-λt
A = 72000 (2,718) -(1,925 x 10-5)
(144000)
A = 4502,65 cacah/s
A = 75,04 cacah/menit
26. Sebuah bahan radioaktif dengan waktu paro 30
menit memberikan laju 50 hitungan/sekon setelah 2 jam. Berapakah laju bahan
radioaktif itu mula-mula?
Diketahui :
T12= 30 menit = 1800s
t = 2 jam = 2 x 3600 = 7200 s
A = 50 hitungan/sekon
Ditanyakan :
A0 =…?
Jawaban :
Tentukan tetapan
peluruhan, λ
T12=ln2λT12=0,693λλ=0,693T12λ=0,6931800λ=3,85×10−4s−1
Cari aktivitas atau laju
bahan radioaktif mula-mula dengan persamaan:
A = A0 e-λt
A0=Ae−λtA0=50e−(3,85×10−4)(7200)A0=50e−2.772A0=799,53≈800hitungan/s
Kesimpulan.
Jadi, laju bahan
radioaktif itu mula-mulai adalah 800 hitungan/sekon.
27. Aktivitas sebuah sumber radioaktif berkurang 1516 bagian dari aktivitas awalnya dalam
selang waktu 1 jam. Tentukan waktu paro dan tetapan peluruhan.
Diketahui :
A=1−1516=116A0
t = 1 jam = 3600s
Ditanyakan :
T12 dan λ =…?
Jawaban :
A=A0(12)n116A0=A0(12)n116=(12)n(12)4=(12)nn=4
Dari n tersebut
dapat dicari waktu paronya dengan:
n=tT12T12=tnT12=14T12=0,25jamT12=15menitT12=900detik
Mencari tetapan
peluruhan adalah dengan:
T12=ln2λT12=0,693λλ=0,693T12λ=0,693900λ=7,7×10−4s−1
Kesimpulan.
Jadi, waktu paronya
adalah 15 menit dan tetapan peluruhannya adalah 7,7 x 10-4 s-1.
28. Kobalt-60 yang waktu paronya 5 tahun sering
digunakan sebagai sumber radiasi dalam bidang kedokteran. Setelah beberapa lama
sejak cuplikan kobalt baru diterima dari pesanan, aktivitasnya kan berkurang
hingga tinggal:
1.
a.
14aktivitas semulanya
b.
116 aktivitas semulanya
Diketahui :
T12=5tahunAa=14A0Ab=116A0
Ditanyakan :
ta dan tb =…?
Jawaban :
A=A0(12)tT12
a.
14aktivitas semulanya
A=A0(12)tT1214A0=A0(12)t514=(12)t5(12)2=(12)t5t5=2t=2×5t=10tahun
b.
116aktivitas semulanya
A=A0(12)tT12116A0=A0(12)t5116=(12)t5(12)4=(12)t5t5=4t=4×5t=20tahun
29. Sebuah laboratorium memiliki 1,43 μg 137Nmurni, yang memiliki waktu paro 10 menit (600 s)
1.
a.
Berapakah banyak inti
yang ada semula ?
b.
Berapa aktivitas radiasi
semula ?
c.
Berapa aktivitasnya
setelah 1,0 jam ?
d.
Berapa lamakah waktu
yang berlangsung hingga aktivitasnya berkurang menjadi 7,42 x 1010 Bq ?
Diketahui :
m = 1,43μg = 1,43 x 10-6 g
T12= 10 menit = 600s
Ditanyakan :
a.
N
b.
A0
c.
A jika t =
1 jam = 3600s
d.
t jika A = 7,42 x 1010 Bq
Jawaban :
a.
Inti semula
Inti
semula dihitung dengan rumus:
N = n x Na
Dengan Na adalah
bilangan avogadro 6,02 x 1023 dan n=aMr maka:
N=aMr×N0
Mr diketahui dari 137N adalah 13, sehingga:
N=1,43×10−613×(6,02×1023)N=6,622×1016
Jadi, banyaknya inti semula yang ada adalah 6,622 x 1016.
b.
Aktivitas semula
Hitung
dulu tetapan peluruhan dengan:
T12=ln2λT12=0,693λλ=0,693×T12λ=0,693×600λ=415,8/s
Maka
aktivitas semula dari 137N adalah :
A0 =
λN
A0 = 415,8 x (6,622 x 1016)
A0 = 2,65 x 1019 molekul/s
A0 = 2,65 x 1019 Bq
Jadi, aktivitas radiasi semuka adalah 2,65 x 109 Bq.
c.
Aktivitas setelah 1 jam
= 3600s
n=tT12n=3600600n=6
A=A0(12)nA=(2,65×1019)×(12)6A=4,14×1017Bq
Jadi, aktivitas radiasi setelah 1 jam adalah 4,14 x 1017 Bq.
d.
t jika A = 7,42 x 1010 Bq
A=A0(12)n(12)n=AA0(12)n=7,42×10102,65×1019(12)n=2,8×10−9(12)28=2,8×10−9n=tT12=28t=nT12t=28×600t=16800st=5jam
Jadi, waktu yang
berlangsung hingga aktivitasnya berkurang menjadi 7,42 x 1010 Bq adalah 5 jam.
30. Suatu isotop 21082Pb yang memiliki waktu paro 11 tahun dibeli 22
tahun yang lalu. Isotop ini akan berubah menjadi 21083Bi. Jika mula-mula terdapat 100 g unsur Pb-210,
tentukan massa Pb-210 dan Bi-83 saat ini.
Diketahui :
T12= 11 tahun
t = 22 tahun
m0 = 100 gram
Ditanyakan :
Massa Pb-210 dan Bi-83
sekarang =…?
Jawaban :
Massa Pb-210 saat ini
adalah massa Pb-210 yang tersisa setelah mengalami peluruhan, yaitu:
m=m0(12)tT12m=100(12)2211m=100(12)2m=100(14)m=25gram
Massa Bi-83 adalah massa
Pb-210 yang telah meluruh membentuk Bi-83 adalah:
m0 – m = 100 – 25
m0 – m = 75 gram
Kesimpulan.
Jadi, massa Pb-210 saat
ini adalah 25 gram, sedangkan massa Bi-83 saat ini adalah 75 gram
31. Suatu contoh radioaktif yang hasil peluruhannya
adalah nonradioaktif, memiliki aktivitas 5 x 1011 Bq
pada suatu waktu. Pada waktu ini detektor partikel α menunjukkan hitungan
dengan laju 32 s-1. Tepat 20 hari kemudian laju hitungan turun
menjadi 8 s-1. Tentukan :
1.
a.
Waktu paro
b.
Tetapan peluruhan
c.
Banyak inti radioaktif
yang ada dalam contoh pada saat awal
d.
Banyak inti radioaktif
yang tertinggal setelah 100 hari dari saat awal
Diketahui :
A = 5 x 1011 Bq
v1 = 32/s
v2 = 8/s
t2 = 20 hari
Ditanyakan :
a.
T12
b.
λ
c.
N0
d.
N jika t = 100 hari
Jawaban :
a.
Waktu paroCari waktu
paro dari laju hitungan pertama dan kedua:
v=v0(12)n8=32(12)n832=(12)n14=(12)nn=2n=tT12T12=tnT12=20hari2T12=10hari
Jadi, waktu paronya adalah 10 hari.
b.
Tetapan peluruhan
T12=ln2λT12=0,693λλ=0,693T12λ=0,69310λ=0,0693
Jadi, tetapan peluruhannya adalah 0,0693
c.
Banyak inti radioaktif
yang ada dalam contoh pada saat awal
A=λNN=AλN0=5×10110,0693N0=7,215×1012
Jadi, banyak inti radioaktif yang ada dalam contoh pada saat awal
adalah 7,215 x 1012.
d.
Banyak inti radioaktif
yang tertinggal setelah 100 hari dari saat awal
N=N0(12)nN=(7,215×1012)×(12)10N=0,7×1012
Jadi, banyak inti
radioaktif yang tertinggal setelah 100 hari dari saat awal adalah 0,7 x 1012.
32. Berapakah aktivitas sebuah wadah yang mengandung
292 cm3 tritium (3H,T12 =23,1 tahun) pada tekanan 5,0 x 105 Pa
(kira-kira 5 atm) pada suhu 300 K? ( R =
8,314 J/mol K).
Diketahui :
V = 292 cm3 =
0,292 L
P = 5,0 x 105 Pa = 5 atm
T = 300 K
R = 8,314 J/mol K
T12 = 23,1 tahun
Ditanyakan :
A =…?
Jawaban :
1.
Menentukan jumlah mol
PV=nRTn=PVRTn=5×0,2928,314×300n=5,85×10−4mol
2.
Mencari inti semula
N = n x Na
Dengan Na adalah
bilangan avogadro 6,02 x 1023 maka:
N = (5,85 x 10-4) x (6,02 x 1023 )
N = 3,5 x 1020
3.
Mencari tetapan
peluruhan
T12=ln2λT12=0,693λλ=0,693T12λ=0,69323,1λ=0,03/hari
4.
Menentukan aktivitas
A = λN
A = 0,03 x (3,5 x 1020)
A = 1,05 x 1029 Bq
Kesimpulan.
Jadi, aktivitas wadah
tersebut adalah 1,05 x 1029 Bq.
33. Suatu bahan memiliki HVL = 3,0 mm untuk
radiasi sinar β. Jika intensitas radiasi ingin dikurangi 90% dari intensitas
semula, tentukan ketebalan bahan yang diperlukan.
Diketahui :
HVL = 3,0 mm
I = I0 – 90%I0 =
10%
Ditanyakan :
x =…?
Jawaban :
Rumus lapisan harga paro, HVL, berkaitan intensitas
sinar radioaktif mirip seperti rumus waktu paro yang berkaitan dengan aktivitas
radiasi yang tertinggal.
A=A0(12)ndengann=tT12miripdenganI=I0(12)ndengann=xHVL
Diketahui HVL =
3,0 mm dan I = I0 –
90%I0 = 0,1I0
Nilai I=I0(12)nsehingga110I0=I0(12)n→(12)3,32=(12)n→n=3,32
Dari rumus n=xHVL diperoleh tebal bahan x = n
x HVL = 3,32 x 3 = 9,96 mm
Kesimpulan.
Jadi, ketebalan bahan
yang diperlukan adalah 9,96 mm.
D.
Aplikasi IPTEK Nuklir
34.
Tentukan nilai Q dari
reaksi-reaksi berikut.
1.
a.
66.0151Li+n→33.0161H+44.0026H
b.
p+22.0141H→2p + n
c.
77.0160Li+2H→88.0053De+n
Diketahui :
Reaksi-reaksi
Ditanyakan :
Nilai Q =…?
Jawaban :
a.
66.0151Li+n→33.0161H+44.0026Hn→neutron→1,009smaSesuai hukum kekekalan
energi maka nilai Q dapat dicari berdasarkan persamaan berikut:
Q = (mreaktan – mproduk)
x 931 MeV/u
Karena
1 sma = 1 u maka dapat diabaikan sehingga :
Q = [(6,0151 +
1,009) – (3,0161 + 4,0026)] x 931
Q = 5,0274 MeV
b.
p+22.0141H→2p + n
n→neutron→1,009smap→proton→1,008sma
Sesuai
hukum kekekalan energi maka nilai Q dapat dicari berdasarkan persamaan berikut
:
Q = (mreaktan – mproduk)
x 931 MeV/u
Karena
1 sma = 1 u maka dapat diabaikan sehingga :
Q = [(1,008 +
2,0141) – (1,008 + 1,009)] x 931
Q = 93,7481 MeV
c.
77.0160Li+2H→88.0053De+n
n→neutron→1,009sma2H→2,014sma
Sesuai hukum kekekalan
energi maka nilai Q dapat dicari berdasarkan persamaan berikut :
Q = (mreaktan – mproduk)
x 931 MeV/u
Karena 1 sma =
1 u maka dapat diabaikan sehingga :
Q = [(7,0160 + 2,014) – (8,0053 + 1,009)] x
931
Q = 14,6167 MeV
35.
Dua reaksi ini yang
terjadi di atmosfer atas adalah :
147N+10n→146C+11H
147N+10n→126C+31H
Hitung energi (dalam
MeV) yang terlibat dalam setiap reaksi.
(N-14 = 14,0031 sma;
C-14 = 14,0032 sma; C-12 = 12,0000 sma; H-3 =
3,0161 sma)
Diketahui :
2 Reaksi:
147N+10n→146C+11H
147N+10n→126C+31H
N-14 = 14,0031 sma;
C-14 = 14,0032 sma; C-12 = 12,0000 sma; H-3 =
3,0161 sma
Ditanyakan :
Q =…?
Jawaban :
(a)147N+10n→146C+11H
Sesuai hukum kekekalan
energi maka nilai Q dapat dicari berdasarkan persamaan beriku t:
Q = (mreaktan – mproduk)
x 931 MeV/u
Dengan nilai n =
1,008665 sma dan H-1 = 1,007825 maka :
Q = [(14,0031 + 1,008665) – (14,0032 +
1,00782)] x 931 =
Q = 0,69 MeV
(b) 147N+10n→126C+31H
Sesuai hukum kekekalan
energi maka nilai Q dapat dicari berdasarkan persamaan berikut:
Q = (mreaktan – mproduk)
x 931 MeV/u
Dengan nilai n =
1,008665 sma maka:
Q = [(14,0031 + 1,008665) – (12,0000 +
3,0161)] x 931
Q =-4,035 MeV
Kesimpulan.
Jadi, energi yang
terlibat dalam setiap reaksi adalah 0,69 MeV dan -4,035 MeV.
36. Manakah reaksi-reaksi inti berikut yang benar ?
1.
a.
126C+21H→146C+42He
b.
147C+10n→126C+11H
c.
73Li+11H→242He
d.
115B+42He→147N+31H
e.
147N+242He→148O+11H
f.
2311Na+42He→178O+11H
Diketahui :
Reaksi – reaksi inti
Ditanyakan :
Reaksi yang benar =…?
Jawaban:
Dalam reaksi peluruhan inti berlaku kekekalan nomor massa,
kekekalan nomor atom, dan kekekalan energi. Maka tidak
akan ada yang berubah nomor massa, nomor atom dan energi dari reaktan (sebelum
reaksi) dengan produk (setelah reaksi). Maka reaksi yang paling benar dapat
ditentukan dari nomor massa dan nomor atomnya :
a.
126C+21H→146C+42He
(Salah)
o Nomor Massa
12 + 2 ≠ 14 + 4
o Nomor Atom
6 + 1 ≠ 6 + 2
b.
147C+10n→126C+11H
(Salah)
o Nomor Massa
14 + 1 ≠ 12 + 1
o Nomor Atom
7 + 0 = 6 + 1
c.
73Li+11H→242He
(Benar)
o Nomor Massa
7 + 1 = 2 x 4
o Nomor Atom
3 + 1 = 2 x 2
d.
115B+42He→147N+31H
(Salah)
o Nomor Massa
11 + 4 ≠ 14 + 3
o Nomor Atom
5 + 2 ≠ 7 + 1
e.
147N+242He→148O+11H
(Salah)
o Nomor Massa
14 + 2 (4) ≠ 14 + 1
o Nomor Atom
7 + 2 (2) ≠ 8 + 1
f.
2311Na+42He→178O+11H
(Salah)
·
- Nomor Massa
23 + 4 ≠ 17 + 1
·
- Nomor Atom
11 + 2 ≠ 8 + 1
Jadi, reaksi inti yang
benar adalah reaksi (c) 73Li+11H→242He
37.
U-235 yang ditembak
dengan neutron lambat sehingga membelah menghasilkan inti Sr-90, inti Xe-140,
dan beberapa buah neutron seperti dinyatakan dalam reaksi berikut :
23592U+n→9038Sr+140aXe+bn
Tentukan nilai a dan b pada
reaksi tersebut.
Diketahui :
23592U+n→9038Sr+140aXe+bn
Ditanyakan :
a dan b =…?
Jawaban :
Dalam hal ini kita menggunakan hukum kekekalan nomor atom dan
nomor massa. Karena neutron memiliki nomor massa dan nomor atom berikut 10n. Nilai a dapat ditentukan dengan hukum
kekekalan nomor atom sebagai berikut:
Nomor atomreaktan =
Nomor atomproduk
92 = 38 + a –> a =
92 – 38 = 54
Nilai b dapat
ditentukan dengan hukum kekekalan nomor massa sebagai berikut:
Nomor massareaktan =
Nomor massaproduk
235 + 1 = 90 + 140
+ b(1)
236 = 230 + 6
–> b = 236 – 230 = 6
Kesimpulan.
Jadi, nilai a =
54 sedangkan nilai b = 6.
38.
Perhatikan reaksi fisi
berikut :
23592U+n→93Rb+141Cs+2n235,043992,9219140,9200
Berapa energi yang
dibebaskan jika :
1.
a.
Fisi terjadi pada 1 atom
saja
b.
Fisi terjadi pada 1 kg
atom?
(Nyatakan dalam kWh)
Diketahui :
23592U+n→93Rb+141Cs+2n235,043992,9219140,9200
Ditanyakan :
a.
Q fisi 1 atom
b.
Q fisi 1 kg
Jawaban :
a.
Energi yang dibebaskan
jika fisi terjadi pada 1 atom saja
Energi
yang dibebaskan jika fisi terjadi pada 1 atom saja dapat ditentukan melalui
persamaan berikut:
Q = Δm x
931MeV/u
Dengan
nilai n = 1,0088665 sma
Q = [(235,0439 +
1,008665) – (92,9219 + 140,200 + 2 (1,008665))] x 931
Q = (236,052565 –
235,13923) x 931
Q = 0,913335 x 931
Q = 850,3 MeV
Jadi, energi yang dibebaskan jika fisi terjadi pada 1 atom
adalah 850,3 MeV.
b.
Energi yang dibebaskan
jika fisi terjadi pada 1 kg atom
235,0439 sma =
235,0439 x (1,66 x 10-27)
235,0439 sma =
3,9 x 10-25 kg
Jika energi yang
dibebaskan untuk 1 atom = 3,9 x 10-25 kg adalah
850,3 MeV maka untuk 1 kg nya adalah:
Q1kg=13,9x10−25x850,3MeVQ1kg=2,18x1027MeVQ1kg=97,02x106kWh
Jadi, energi yang
dibebaskan jika fisi terjadi pada 1 kg atom adalah 97,02 x 106 kWh.
39. Apabila suatu atom 235U
mengalami fisi dalam reaktor, energi sebesar 200 MeV dibebaskan. Misalkan suatu
reaktor yang memakai 235U memiliki efisiensi 25% dan
menghasilkan daya 800 MW.
1.
a.
Berapa banyak atom
uranium yang terpakai setiap hari sebagai bahan bakar reaktor ?
b.
Berapakah massa uranium
yang dibakar tiap hari ?
Diketahui :
235U –> Ar = 235
E1 = 200 MeV = 200 x 106 x
1,6 x 10-19 J
η = 25% = 0,25
P = 800 MW = 800 x 106 W
t = 1 hari = 24 x 3600 =
86400s
Ditanyakan :
a.
jumlah atom (n)
b.
m
Jawaban :
a.
Banyaknya atom uranium
yang terpakai dalam setiap hari (n)
Berdasarkan
hukum kekekalan energi, maka :
Ereaktor = Efusi
P x t =
η x n x E1
(800
x 106) x 86400 = 0,25 x n x (200 x 106 x
1,6 x 10-19)
6,912
x 1013 = 8 x 10-12 n
n=6,912×10138×10−12n=8,64×1024
b.
Massa uranium tiap hari
JumlahPartikelNA=mArm=JumlahPartikel×ArNA
Dengan nilai NA =
6,02 x 1023 maka :
m=(8,64×1024)×2356,02×1023m=3372,75gramm=3,37kg
Kesimpulan.
Jadi, uraniom yang terpakai setiap hari sebagain bahan bakar
reaktor adalah 8,64 x 1024 atom. Sedangkan massa uranium yang
dibakar tiap hari adalah 3,37 kg.
40. Jika 1 kg batu bara dibakar,
kira-kira 3 x 107 J energi dibebaskan. Jika energi
yang dibebaskan tiap fisi satu atom 23592U adalah 2 x 102 MeV, berapa kg batu bara
harus dibakar untuk memproduksi energi yang sama dengan energi fisi dari
1 kg 23592U?
Diketahui :
1 kg batu bara –> 3 x
107 J = 3x1071.6x10−19= 1,875 x 1026 eV =
1,875 x 1020 MeV
1 atom 23592U–> 2 x 102 MeV
Ditanyakan :
n batu bara =…?
Jawaban :
Setiap fisi 1 atom 23592U adalah 2 x 102 MeV maka
artinya :
235,0429 sma =
235,0439 x (1,66 x 10-27) = 3,9 x 10-25 kg
Untuk 1 kg 23592U energi yang dibebaskan adalah :
Q1kg=13,9×10−25×200MeVQ1kg=5,128×1026MeV
Jika 1 kg batu bara melepaskan 1,875 x 1020 MeV maka
untuk menyamakan dengan 1 kg 23592U dibutuhkan:
nbatubara=1kg23592U1kgbatubaran=5,128×10261,875×1020n=2,74×106batubara
Kesimpulan.
Jadi, batu bara harus dibakar untuk memproduksi energi yang sama
dengan energi fisi dari 1 kg 23592U adalah 2,74 x 106 Kg batu bara.
41.
Uranium 23592U membelah menjadi dua inti ditambah dengan tiga neutron.
10n+23592U→(2inti)+310n
Massa 23592U= 235,0439 u.
Jika energi dibebaskan selama reaksi fisi (pembelahan)
berlangsung, berapakah massa gabungan kedua inti yang terbentuk ?
Diketahui :
Reaksi fisi :
10n+23592U→(2inti)+310n
Massa 23592U= 235,0439 u
Q = 225 MeV
Ditanyakan :
Massa 2 inti =…?
Jawaban :
Dari persamaan reaksi :
10n+23592U→(2inti)+310n
Didapatkan :
Q = Δm x 931 MeV/u
Dengan nilai n =
1,008665 sma
225 = [(1,008665 +
235,0439) – (2 inti + 3(1,008665)] x 931
225 = [(236,052565 – (2
inti + 3,025995)] x 931
225931= 233,02657 – 2 inti
0,24167 = 233,02657 – 2
inti
2 inti = 233,02657 –
0,24167
2 inti = 232,7849 sma
2 inti = 232,7849 u
Kesimpulan.
Jadi, massa gabungan
kedua inti yang terbentuk adalah 232,7849 u.
42. Reaksi fusi yang terjadi dalam Matahari dan
menghasilkan energi yang besar dinyatakan dalam reaksi 411H→42He+20+1e+energi, dengan 0+1e adalah sebuah positron (elektron bermuatan
positif). Berapa besar energi yang dibebaskan jika 1 kg hidrogen
telah dikonsumsi ?
Diketahui :
411H→42He+20+1e+energi
Ditanyakan :
E untuk 1 kg H =…?
Jawaban :
11H=1,007825u42He=4,002602u0+1e=0,000549u
Q = (mreaktan – mproduk)
x 931 MeV/u
Q = [(4 x 1,007825) – ((4,002602) – (2 x
0,000549))] x 931 MeV
Q = 0,0276 x 931 MeV
Q = 25,7 MeV
Kesimpulan.
Jadi, besar energinya
adalah 25,7 MeV.
43. Isotop C-14 memiliki waktu paro 5.600 tahun.
Sewaktu hidup tumbuh-tumbuhan menyerap dan memancarkan C-14 (dalam bentuk
karbon dioksida) sehingga jumlah isotop tetap.
1.
a.
Apa yang terjadi dengan
jumlah C-14 setelah tumbuh-tumbuhan tersebut mati ?
b.
Sebuah contoh kayu yang
ditemukan pada suatu kota purba memberi aktivitas radiasi karbon-14 sebesar 36
hitungan per menit. Sebuah contoh kayu sejenis yang masih hidup memberikan
aktivitas radiasi sebesar 72 hitungan per menit. Perkirakan umur kayu ini.
Diketahui :
Isotop C-14 memiliki
waktu paro 5.600 tahun
Ditanyakan :
a.
Apa yang terjadi dengan
jumlah C-14 setelah tumbuh-tumbuhan tersebut mati?
b.
Perkiraan umur kayu
Jawab:
a.
Apa yang terjadi dengan
jumlah C-14 setelah tumbuh-tumbuhan tersebut mati?
Karbon-14 (C-14) yang mempunyai waktu paro 5.600 tahun dibentuk di
atmosfer oleh partikel-partikel yang mempunyai energi tinggi yang beasal dari
angkasa luar. Partikel-partikel berenergi tinggi ini disebut sinar-sinar
kosmis. Tumbuhan, binatang, dan manusia menyerap dan mengeluarkan karbon-14
selama mereka masih hidup. Oleh karena itu, persentase karbon-14 dalam tubuh
mereka selalu tetap. Ketika mereka (tumbuhan, binatang, manusia) mati,
persentase karbon-14 berkurang karena inti C-14 meluruh dengan memancarkan
sinar beta. Dengan mengukur persentase keaktifan radiasi C-14 dalam tumbuhan,
binatang, atau manusia yang mati, kita dapat menaksir umur kematian mereka.
Teknik seperti inilah yang disebut penentuan umur dengan radioaktif.
b.
Diketahui :
T12=5600 tahun
A = 36 hitungan/menit
A0 = 72 hitungan per menit
Ditanyakan :
t =…?
Jawaban :
t=ln(AA0)−0,693×T12
t=ln(3672)−0,693×5600t=5600tahun
Kesimpulan.
Jadi, perkiraan umur
kayu ini adalah 5.600 tahun.
44. Sebuah rumah tertentu menggunakan kira-kira
2.000 kWh energi listrik per bulan. Berapa banyak inti yang
harus mengalami reaksi fusi 21H+31H→42He+10nuntuk memenuhi
kebutuhan energi listrik rumah itu selama 1 tahun ?
(Massa 21H=2,0141sma;31H=3,0161sma;42He=4,0026sma+10n=1,0086sma;1sma=930Mev)
Diketahui :
Persamaan reaksi
fusi 21H+31H→42He+10n
21H=2,0141sma31H=3,0161sma42He=4,0026sma10n=1,0086sma1sma=930Mev
2.000 kWh/bulan
Ditanyakan :
n =…?
Jawaban :
Menentukan energi dari
persamaan reaksi fusi :
E = [(2,0141 + 3,0161) – (4,0026 + 1,0086)]
x 931
E = 17,689 MeV
Ubah MeV ke
satuan Joule :
17,689 MeV =
(17,689 x 106 eV) x (1,6 x 10-19)
17,689 MeV =
2,83 x 10-12 Joule
Yang dibutuhkan dalam
setahun :
2000 kWh/bulan –>
1 tahun = 12 x 2000 kWh = 24000 kWh
24000 kWh =
24000 x 3600 kJ
24000 kWh =
86,4 x 109 Joule
n=86,4×1092,83×10−12n=3×1022
Kesimpulan.
Jadi, untuk memenuhi kebutuhan energi listrik rumah itu selama 1
tahun dibutuhkan 3 x 1022 inti yang harus bereaksi.
45. Sebuah contoh batuan tertentu mengandung 206Pb
dan 238U perbandingan berat 1:5. Uranium memiliki waktu paro
1,4 x 1017 s. Hitung :
1.
a.
Banyak atom-atom 206Pb
dan 238U dalam suatu contoh batuan yang mengandung 1 g 238U.
b.
Massa 238U
awal dalam contoh batuan ini.
c.
Usia batuan.
Diketahui :
206Pb dan 238U
T12U= 1,4 x 1017 s
w 206Pb
:w 238U = 1 : 5
Ditanyakan :
Tentukan :
a.
Banyaknya atom 206Pb
dan 238U dalam suatu contoh batuan yang mengandung 1 g 238U
b.
m0238U
c.
t
Jawaban :
a.
Jawaban :Istilah
radioactive dating digunakan pada penggunaan radiasi dari unsur
radioaktif untuk menentukan umur atau usia (dating) suatu bahan yang
mengandung unsur radioaktif tersebut. Misalnya batuan yang semula
mengandung 238U dapat ditentukan umurnya
dengan menghitung kadar 206Pb pada batuan
sekarang. 238U akan berhenti meluruh jika telah
terbentuk 206Pb.
23892U→20682Pb+842He+60−1e
Jadi setiap 238 gram 238U setelah berhenti
meluruh akan menghasilkan 206 gram 206P. Waktu paruh 238Uadalah
4,5 x 109 tahun. Setelah 4,5 x 109 tahun, 1
gram 238U akan mengahsilkan (½ x 1 = 0,5) gram 238U dan( ½
x 206 ⁄ 238= 0,43) gram 206P. Jika
dimisalkan sedikit sampel batuan tersebut mengandung 1 gram 238U dan
0,76 gram 206P, maka :
b.
m0238Um0238U
= 1+(238206×0,76)gram=1,88gram
c.
t
Dapat dicari dengan
persamaan :
ln11,88ln=−0,6934,5×109xt
Jadi umur batuan
tersebut :
t=(4,5×1090,693)xln11,88tahunt=4,099×109tahun


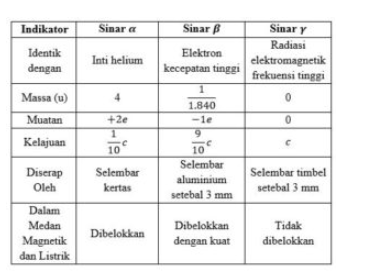

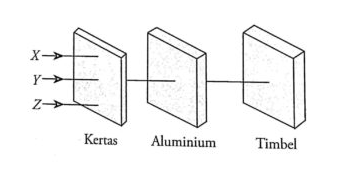











No comments:
Post a Comment